Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0097 จาก 0508
| กระทู้ที่ 0096 ส่งของตอบแทนไปให้คนที่แจ้งข้อแก้ไขแล้วครับ | ตั้งกระทู้ใหม่ | กระทู้ที่ 0098 พหุนาม |
มีข้อสงสัย เกี่ยวกับโจทย์ในหนังสือ หน้า 146 ครับ !!!ตอบ: 3, อ่าน: 9706, แท็ก: แจ้งจุดผิด, ถามโจทย์, ฟังก์ชัน, โดเมน, เรนจ์
ผมมีข้อสงสัยเล็กน้อย เกี่ยวกับโจทย์ในหนังสือ ตอนท้ายของหน้า 146 ผมได้ลองกลับไปคิดโจทย์ข้อนี้ดู และแสดงวิธีทำออกมา โดยใช้วิธีตามที่พี่ได้แนะนำไว้ สำหรับการหาโดเมนของฟังก์ชันคอมโพสิท ผมได้คำตอบตรงกับที่พี่ได้ให้คำตอบไว้ แต่สำหรับเรนจ์ผมได้คำตอบไม่ตรงกับที่พี่ให้คำตอบไว้ครับ ซึ่งไม่ทราบว่าผมแสดงวิธีทำผิดตรงขั้นตอนไหนหรือเปล่า และไม่แน่ใจว่า วิธีการที่ผมทำนั้นถูกต้องหรือไม่ ดังนั้นผมขอให้พี่ผู้เขียนกรุณาช่วยตรวจสอบวิธีทำของผมด้วยนะครับว่าถูกต้องหรือไม่ แต่อย่างไรแล้วผมก็ได้แนวความคิดในการหาโดเมนและเรนจ์ของฟังก์ชันคอมโพสิท ตามที่พี่ได้แนะนำไว้ในหนังสือเป็นอย่างดีครับ
ท้ายที่สุดนี้ ผมต้องขอขอบพระคุณพี่ผู้เขียนเป็นอย่างสูง ที่ได้สละเวลาสร้างสรรหนังสือคณิตศาสตร์ที่ดีๆ อย่างนี้ให้พวกเราเหล่านักเรียนได้อ่านกัน ผมอยากให้ผู้เขียนแต่งตำราดีๆ แบบนี้ขึ้นมาอีก ผมขอเป็นกำลังใจ และจะติดตามผลงานวิชาการของพี่เสมอครับ
ด้านล่างนี้ผมได้แสดงวิธีทำโจทย์ข้อนี้ไว้ พี่กรุณาแนะนำผมด้วยว่าผมแสดงวิธีทำตามที่พี่สอน มาได้ถูกต้องหรือผิดพลาดอย่างไร


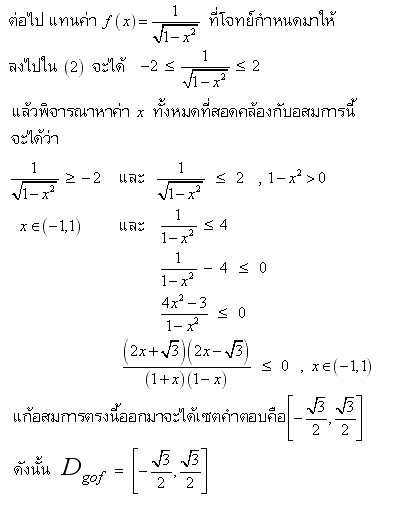


ขอบคุณมากครับ
Eddie
ท้ายที่สุดนี้ ผมต้องขอขอบพระคุณพี่ผู้เขียนเป็นอย่างสูง ที่ได้สละเวลาสร้างสรรหนังสือคณิตศาสตร์ที่ดีๆ อย่างนี้ให้พวกเราเหล่านักเรียนได้อ่านกัน ผมอยากให้ผู้เขียนแต่งตำราดีๆ แบบนี้ขึ้นมาอีก ผมขอเป็นกำลังใจ และจะติดตามผลงานวิชาการของพี่เสมอครับ
ด้านล่างนี้ผมได้แสดงวิธีทำโจทย์ข้อนี้ไว้ พี่กรุณาแนะนำผมด้วยว่าผมแสดงวิธีทำตามที่พี่สอน มาได้ถูกต้องหรือผิดพลาดอย่างไร


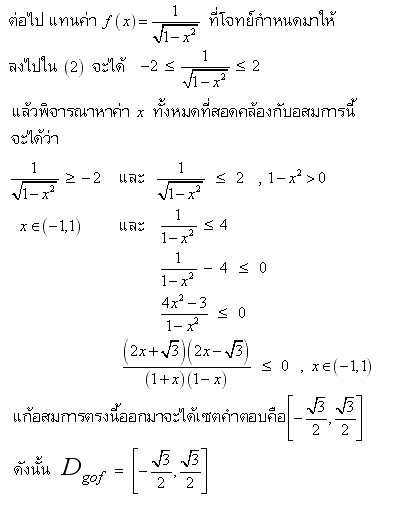


ขอบคุณมากครับ
Eddie
eddy_thai2004@yahoo.com 16/02/49 19:03
ปรากฏว่าเน็ตของ tot ที่ผมใช้ดันมีปัญหาเอาตอนนี้พอดี
ผมเปิดเว็บของเมืองนอกไม่ได้เลย
รูปภาพที่น้อง eddie เอามาแปะก็เลยยังเปิดไม่ได้
แต่ได้ตรวจเช็คโจทย์ข้อนี้อีกครั้งแล้วครับ
ก็พบว่า เฉลยของเรนจ์ต้องแก้เป็น [0,รู้ท3] ครับ
อันนี้ผมเคยแก้ไว้ด้วยดินสอ แล้วดันลืมแก้ในไฟล์อ่ะ..
คิดว่าน้อง eddie ก็คงจะได้คำตอบเท่านี้เหมือนกันนะครับ
ขอบคุณที่แจ้งข้อแก้ไขครับ :]
(ส่งของตอบแทนไปให้ทางอีเมล์แล้วครับ)
ผมเปิดเว็บของเมืองนอกไม่ได้เลย
รูปภาพที่น้อง eddie เอามาแปะก็เลยยังเปิดไม่ได้
แต่ได้ตรวจเช็คโจทย์ข้อนี้อีกครั้งแล้วครับ
ก็พบว่า เฉลยของเรนจ์ต้องแก้เป็น [0,รู้ท3] ครับ
อันนี้ผมเคยแก้ไว้ด้วยดินสอ แล้วดันลืมแก้ในไฟล์อ่ะ..
คิดว่าน้อง eddie ก็คงจะได้คำตอบเท่านี้เหมือนกันนะครับ
ขอบคุณที่แจ้งข้อแก้ไขครับ :]
(ส่งของตอบแทนไปให้ทางอีเมล์แล้วครับ)
นวย 16/02/49 20:16 [ 1 ]
ตอนนี้ผมเปิดดูวิธีทำของน้อง eddie ได้แล้ว
ความเข้าใจทั้งหมดนั้นถูกต้องแล้วครับ :]
มีวิธีคิดที่สั้นลงมาเสนอครับ
หาโดเมน
จาก (gof)(x) = รู้ท (4 - f(x)2)
มองเงื่อนไขของรู้ท จะได้ 4 - f(x)2 > 0
f(x)2 < 4
-2 < f(x) < 2
แปลว่า -2 < 1 / รู้ท(1 - x2) < 2
แต่ 1/รู้ท ย่อมมากกว่า -2 อยู่แล้วเสมอ (เป็นจริงทุกค่า x)
ดังนั้นเราคิดเฉพาะซีกขวามือก็พอ
1 / รู้ท(1 - x2) < 2
คูณไขว้ได้เพราะทราบว่าเป็นค่าบวกแน่นอน (แต่ต้องเขียนกำกับว่า x ห้ามเป็น -1 หรือ 1)
1/2 < รู้ท(1 - x2)
1/4 < 1 - x2
x2 < 3/4
ดังนั้น x อยู่ในช่วง [-รู้ท3 /2, รู้ท3 /2]
ความเข้าใจทั้งหมดนั้นถูกต้องแล้วครับ :]
มีวิธีคิดที่สั้นลงมาเสนอครับ
หาโดเมน
จาก (gof)(x) = รู้ท (4 - f(x)2)
มองเงื่อนไขของรู้ท จะได้ 4 - f(x)2 > 0
f(x)2 < 4
-2 < f(x) < 2
แปลว่า -2 < 1 / รู้ท(1 - x2) < 2
แต่ 1/รู้ท ย่อมมากกว่า -2 อยู่แล้วเสมอ (เป็นจริงทุกค่า x)
ดังนั้นเราคิดเฉพาะซีกขวามือก็พอ
1 / รู้ท(1 - x2) < 2
คูณไขว้ได้เพราะทราบว่าเป็นค่าบวกแน่นอน (แต่ต้องเขียนกำกับว่า x ห้ามเป็น -1 หรือ 1)
1/2 < รู้ท(1 - x2)
1/4 < 1 - x2
x2 < 3/4
ดังนั้น x อยู่ในช่วง [-รู้ท3 /2, รู้ท3 /2]
นวย 16/02/49 21:13 [ 2 ]
ต่อไป หาเรนจ์นะครับ..
มีวิธีคิดเรนจ์ f(x) แบบลัดๆ โดยเริ่มจาก x เป็นจำนวนจริงใดๆ
แล้วค่อยๆ ทำให้กลายเป็น f(x) โดยพิจารณาตัดช่วงที่เป็นไปไม่ได้ออกทีละขั้นๆ
x เป็นจำนวนจริงใดๆ
ยกกำลังสอง จะได้ ... x2 > 0 เสมอ
เอา 1 มาลบข้างหน้า จะได้ ... 1 - x2 < 1 เสมอ
จากนั้นใส่รู้ท จะได้ ... 0 < รู้ท(1 - x2) < 1
(ต้องใส่ 0 กำกับไว้ทางซ้ายด้วยนะครับ เพราะรู้ทจะติดลบไม่ได้)
ต่อมาก็เอา 1 มาหารด้านบน
จะได้ ... 1 < 1 / รู้ท(1 - x2) < อินฟินิตี้
นั่นคือ f(x) > 1 เสมอ.. นี่คือเรนจ์ของ f ครับ
แล้วเราก็เอาช่วงเรนจ์ของ f นี้ไปทำให้เหมือน gof ต่อ..
f(x)2 > 1
เอา 4 ไปลบด้านหน้า จะได้ ... 4 - f(x)2 < 3
ใส่รู้ทครับ ... 0 < รู้ท(4 - f(x)2) < รู้ท3
(ต้องใส่ 0 กำกับไว้ทางซ้ายเหมือนเดิมครับ เพราะรู้ทติดลบไม่ได้)
นั่นคือ (gof)(x) อยู่ในช่วง [0, รู้ท3] ครับผม..
:]
มีวิธีคิดเรนจ์ f(x) แบบลัดๆ โดยเริ่มจาก x เป็นจำนวนจริงใดๆ
แล้วค่อยๆ ทำให้กลายเป็น f(x) โดยพิจารณาตัดช่วงที่เป็นไปไม่ได้ออกทีละขั้นๆ
x เป็นจำนวนจริงใดๆ
ยกกำลังสอง จะได้ ... x2 > 0 เสมอ
เอา 1 มาลบข้างหน้า จะได้ ... 1 - x2 < 1 เสมอ
จากนั้นใส่รู้ท จะได้ ... 0 < รู้ท(1 - x2) < 1
(ต้องใส่ 0 กำกับไว้ทางซ้ายด้วยนะครับ เพราะรู้ทจะติดลบไม่ได้)
ต่อมาก็เอา 1 มาหารด้านบน
จะได้ ... 1 < 1 / รู้ท(1 - x2) < อินฟินิตี้
นั่นคือ f(x) > 1 เสมอ.. นี่คือเรนจ์ของ f ครับ
แล้วเราก็เอาช่วงเรนจ์ของ f นี้ไปทำให้เหมือน gof ต่อ..
f(x)2 > 1
เอา 4 ไปลบด้านหน้า จะได้ ... 4 - f(x)2 < 3
ใส่รู้ทครับ ... 0 < รู้ท(4 - f(x)2) < รู้ท3
(ต้องใส่ 0 กำกับไว้ทางซ้ายเหมือนเดิมครับ เพราะรู้ทติดลบไม่ได้)
นั่นคือ (gof)(x) อยู่ในช่วง [0, รู้ท3] ครับผม..
:]
นวย 16/02/49 21:22 [ 3 ]