Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0229 จาก 0508
| กระทู้ที่ 0228 มาขอบคุณและสอบถาม | ตั้งกระทู้ใหม่ | กระทู้ที่ 0230 รออ่านฉบับ ขี้หลอกอยู่นะคะ แอดปี 51 อ่ะ |
ขอแนวคิด วิธีทำ โจทย์คณิตศาสตร์ ม.ต้น ด้วยครับตอบ: 5, อ่าน: 15313, แท็ก: ถามโจทย์, เรขาคณิตวิเคราะห์, ตรีโกณมิติ
พี่นวยครับผมขอแนวคิดโจทย์ข้อต่อไปนี้ด้วยครับ
เป็นข้อสอบแข่งขันของ ม.ต้น ครับ


ขอบคุณมากครับ 😀
เป็นข้อสอบแข่งขันของ ม.ต้น ครับ


ขอบคุณมากครับ 😀
Eddie 03/12/50 15:56
ข้อ 31 เราลองคิดมั่วๆ ดู 2 วิธี
ได้พท.แรเงาเป็น 0.46 ทั้ง 2 วิธีเลยอะ (ใช้ pi=3.14, root 3= 1.732)
เลยไม่รู้ว่าถ้าแทนค่าละเอียดกว่านี้ มันจะเข้าใกล้ 0.4 หรือ 0.5 มากกว่ากัน - -'
หรือมันผิดทั้ง 2 วิธีเลยก็ไม่รู้สิแฮะ
ข้อ 34 ทำไม่เป็น แต่ขอฟันธงว่าคำตอบต้องอยู่ระหว่างข้อ 3 4 5 แน่นอน :P
ได้พท.แรเงาเป็น 0.46 ทั้ง 2 วิธีเลยอะ (ใช้ pi=3.14, root 3= 1.732)
เลยไม่รู้ว่าถ้าแทนค่าละเอียดกว่านี้ มันจะเข้าใกล้ 0.4 หรือ 0.5 มากกว่ากัน - -'
หรือมันผิดทั้ง 2 วิธีเลยก็ไม่รู้สิแฮะ
ข้อ 34 ทำไม่เป็น แต่ขอฟันธงว่าคำตอบต้องอยู่ระหว่างข้อ 3 4 5 แน่นอน :P
Shauฯ (จะตอบทำไม) 04/12/50 22:33 [ 1 ]
ข้อ 31. พี่นวยได้ 5pi/12 - (รู้ท3)/2
ประมาณค่าได้ 0.442 เลยไม่รู้จะตอบ 0.4 หรือ 0.5 ดีกว่ากัน
ส่วนข้อ 34. ก็ยังคิดไม่ออกเหมือนกัน ขอเวลาต่ออีกหน่อยนะครับ..
(แต่ถ้าใครคิดได้หรือรู้เฉลยแล้ว ไม่ต้องรอกันครับ ขอเชิญแสดงฝีมือโลด!)
แนวคิดข้อ 31. ก็เอามาจากข้อสอบพื้นฐานวิศวะ 2533 (ข้อ 17.) ใน Math E-Book นี่แหละครับ
ถ้ารู้วิธีทำข้อนั้นแล้ว เอามาขยายผลทำข้อนี้ได้สบายเลย..
ป.ล. แล้วน้องชอฯ ทำวิธีไหนเหรอ พี่นวยคิดตั้งนานได้แค่วิธีเดียวเองอ่ะ
ประมาณค่าได้ 0.442 เลยไม่รู้จะตอบ 0.4 หรือ 0.5 ดีกว่ากัน
ส่วนข้อ 34. ก็ยังคิดไม่ออกเหมือนกัน ขอเวลาต่ออีกหน่อยนะครับ..
(แต่ถ้าใครคิดได้หรือรู้เฉลยแล้ว ไม่ต้องรอกันครับ ขอเชิญแสดงฝีมือโลด!)
แนวคิดข้อ 31. ก็เอามาจากข้อสอบพื้นฐานวิศวะ 2533 (ข้อ 17.) ใน Math E-Book นี่แหละครับ
ถ้ารู้วิธีทำข้อนั้นแล้ว เอามาขยายผลทำข้อนี้ได้สบายเลย..
ป.ล. แล้วน้องชอฯ ทำวิธีไหนเหรอ พี่นวยคิดตั้งนานได้แค่วิธีเดียวเองอ่ะ
นวย 05/12/50 01:43 [ 2 ]
แหะๆ ตอนแรกไม่รู้จะหาพท. MOAP ยังไง เลยมั่วนิ่มคิดเป็นสี่เหลี่ยมผืนผ้าไปก่อนน่ะค่ะ
แต่ตอนหลังคิดใหม่เป็นสามเหลี่ยม OMP กะ 1/12 ของวงกลม OPA เลยได้ 5pi/12- (root3)/2 เหมือนกันค่ะ
แต่ตอนหลังคิดใหม่เป็นสามเหลี่ยม OMP กะ 1/12 ของวงกลม OPA เลยได้ 5pi/12- (root3)/2 เหมือนกันค่ะ
Shauฯ(6) 05/12/50 11:22 [ 3 ]
ข้อ 34. สุดท้ายพี่นวยก็ต้องไปพึ่งตรีโกณมิติ (สูตร arctan) อ่ะครับ ถึงจะได้คำตอบ
..ซึ่งมันเกินหลักสูตร ม.ต้น แน่นอน ก็เลยคิดว่าคงมีวิธีที่ง่ายกว่านี้มั้งครับ
จากโจทย์ ให้ O เป็นจุดศูนย์กลางวงกลม แล้วลากเส้น AB, BC, AO, OC ..ดังรูป
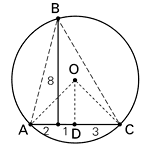
(1) หาขนาดมุม ABC ได้จากสามเหลี่ยมมุมฉากซีกซ้ายและขวา
นั่นคือ ABC = arctan (2/8) + arctan (4/8)
ใช้สูตรผลบวก arctan แล้วจะได้ผลเป็น arctan (6/7) ---- ตรงนี้ล่ะที่เกินหลักสูตร ม.ต้น
(2) จากสมบัติของสามเหลี่ยมแนบในวงกลม จึงทราบว่าขนาดมุม AOC = 2 ABC
แต่สามเหลี่ยม AOC เป็นสามเหลี่ยมหน้าจั่ว แสดงว่า AOD = ครึ่งของAOC
ดังนั้น AOD ก็เลยเท่ากับ ABC ..นั่นคือ arctan (6/7) เช่นกัน
(3) จากสามเหลี่ยม AOD ก็จะหาความยาวรัศมีวงกลม (ซึ่งในที่นี้คือ AO) ได้ดังนี้
รัศมี (AO) = AD / sin AOD
= 3 / (6/รู้ท85) = (รู้ท85)/2 ขอตอบครับ..
ป.ล.1 สูตร arctan เป็นดังนี้ครับ
arctan x + arctan y = arctan [ (x + y) / (1 - xy) ]
และ arctan x - arctan y = arctan [ (x - y) / (1 + xy) ]
ป.ล.2 น้องชอฯ คงชอบเลย คำตอบนี้.. อิๆๆ..
ป.ล.3 ปรากฏว่าวิธีข้อ 31. ของคุณน้องชอฯ (สามเหลี่ยม OMP กับชิ้นวงกลมมุม 30 องศา OPA)
แจ่มกว่าวิธีของพี่นวย (พื้นที่ส่วนเสี้ยววงกลม MBP) อยู่หลายขุมเลยครับ.. 😁
..ซึ่งมันเกินหลักสูตร ม.ต้น แน่นอน ก็เลยคิดว่าคงมีวิธีที่ง่ายกว่านี้มั้งครับ
จากโจทย์ ให้ O เป็นจุดศูนย์กลางวงกลม แล้วลากเส้น AB, BC, AO, OC ..ดังรูป

(1) หาขนาดมุม ABC ได้จากสามเหลี่ยมมุมฉากซีกซ้ายและขวา
นั่นคือ ABC = arctan (2/8) + arctan (4/8)
ใช้สูตรผลบวก arctan แล้วจะได้ผลเป็น arctan (6/7) ---- ตรงนี้ล่ะที่เกินหลักสูตร ม.ต้น
(2) จากสมบัติของสามเหลี่ยมแนบในวงกลม จึงทราบว่าขนาดมุม AOC = 2 ABC
แต่สามเหลี่ยม AOC เป็นสามเหลี่ยมหน้าจั่ว แสดงว่า AOD = ครึ่งของAOC
ดังนั้น AOD ก็เลยเท่ากับ ABC ..นั่นคือ arctan (6/7) เช่นกัน
(3) จากสามเหลี่ยม AOD ก็จะหาความยาวรัศมีวงกลม (ซึ่งในที่นี้คือ AO) ได้ดังนี้
รัศมี (AO) = AD / sin AOD
= 3 / (6/รู้ท85) = (รู้ท85)/2 ขอตอบครับ..
ป.ล.1 สูตร arctan เป็นดังนี้ครับ
arctan x + arctan y = arctan [ (x + y) / (1 - xy) ]
และ arctan x - arctan y = arctan [ (x - y) / (1 + xy) ]
ป.ล.2 น้องชอฯ คงชอบเลย คำตอบนี้.. อิๆๆ..
ป.ล.3 ปรากฏว่าวิธีข้อ 31. ของคุณน้องชอฯ (สามเหลี่ยม OMP กับชิ้นวงกลมมุม 30 องศา OPA)
แจ่มกว่าวิธีของพี่นวย (พื้นที่ส่วนเสี้ยววงกลม MBP) อยู่หลายขุมเลยครับ.. 😁
นวย 06/12/50 00:21 [ 4 ]
อิอิ คำตอบข้อ 34 แจ่มจริงๆ ด้วยค่ะ
ถ้าสอบเอง ถึงคิดไม่ออกก็คงได้คะแนนข้อนี้ชัวร์ 😄
...ทำเป็นเล่นไป สมัยเอนท์เคยมั่วเคมีเติมคำข้อละ 5 (เอ๊ะ หรือ 3 ??) คะแนนถูกด้วยนะเออ ภูมิใจยิ่งกว่าข้อที่คิดออกเองอีก 55
ถ้าสอบเอง ถึงคิดไม่ออกก็คงได้คะแนนข้อนี้ชัวร์ 😄
...ทำเป็นเล่นไป สมัยเอนท์เคยมั่วเคมีเติมคำข้อละ 5 (เอ๊ะ หรือ 3 ??) คะแนนถูกด้วยนะเออ ภูมิใจยิ่งกว่าข้อที่คิดออกเองอีก 55
Shauฯ(6) 06/12/50 09:28 [ 5 ]