Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0269 จาก 0508
| กระทู้ที่ 0268 แจ้งข้อแก้ไข สำหรับRelease 2.9 preview#1 ครับ | ตั้งกระทู้ใหม่ | กระทู้ที่ 0270 แนะนำตัว |
ขอวิธีคิดและแนวคิดที่หลากหลายหน่อยนะครับ (กฎเกณฑ์เบื้องต้นเกี่ยวกับการนับ)ตอบ: 7, อ่าน: 180888, แท็ก: ถามโจทย์, ความน่าจะเป็น
ข้อ1.
นำเลขโดด 1 ถึง 9 สร้างจำนวนคู่บวก ที่มี 5 หลัก
แต่ละหลักซ้ำกันได้ จะสามารถสร้างได้กี่จำนวน
ข้อ2.
ต้องการสร้างจำนวนคู่ 4 หลัก จากเลขโดด 0 ถึง 5
โดยในแต่ละหลักเลขไม่ซ้ำกัน จะสร้างได้กี่จำนวน
ข้อ3.
ต้องการสร้างจำนวนคี่ 4 หลัก จากเลขโดด 0 ถึง 5
โดยในแต่ละหลักเลขไม่ซ้ำกัน จะสร้างได้กี่จำนวน
ข้อ4.
ส่งจดหมาย 4 ฉบับ ใส่ตู้รับ 3 ตู้ จะมีวิธีการส่งกี่วิธี
ข้อ5.
รถคันหนึ่ง นั่งหน้าได้ 3 คน นั่งหลัง ได้ 4 คน
ถ้ามีคนทั้งหมด 7 คน ขับรถไม่เป็น 3 คน
จะจัดที่นั้งได้ทั้งหมดกี่วิธี
ข้อ6.
ห้องประชุมมีประตู 4 ประตู ถ้านาย ก. และ ข.
จะเดินเข้าและออกห้องประชุม ได้กี่วิธีเมื่อ (ก.และ ข.ไม่ได้เดินไปด้วยกัน)
6.1 ทั้งสองจะเข้าและออกประตูใดก็ได้
6.2 แต่ละคนเข้าประตูใด จะออกประตูนั้นไม่ได้
6.3 ทั้งสองจะใช้วิธีการเข้าและออกเหมือนกันไม่ได้
ข้อ7.
สร้างจำนวน 4 หลัก แต่หลักใช้เลขซ้ำกันไม่ได้ โดยใช้เลข 0 ถึง 9
ให้เป็นจำนวนคี่ ระหว่าง 2,000 - 6,000 จะสร้างได้กี่จำนวน
นำเลขโดด 1 ถึง 9 สร้างจำนวนคู่บวก ที่มี 5 หลัก
แต่ละหลักซ้ำกันได้ จะสามารถสร้างได้กี่จำนวน
ข้อ2.
ต้องการสร้างจำนวนคู่ 4 หลัก จากเลขโดด 0 ถึง 5
โดยในแต่ละหลักเลขไม่ซ้ำกัน จะสร้างได้กี่จำนวน
ข้อ3.
ต้องการสร้างจำนวนคี่ 4 หลัก จากเลขโดด 0 ถึง 5
โดยในแต่ละหลักเลขไม่ซ้ำกัน จะสร้างได้กี่จำนวน
ข้อ4.
ส่งจดหมาย 4 ฉบับ ใส่ตู้รับ 3 ตู้ จะมีวิธีการส่งกี่วิธี
ข้อ5.
รถคันหนึ่ง นั่งหน้าได้ 3 คน นั่งหลัง ได้ 4 คน
ถ้ามีคนทั้งหมด 7 คน ขับรถไม่เป็น 3 คน
จะจัดที่นั้งได้ทั้งหมดกี่วิธี
ข้อ6.
ห้องประชุมมีประตู 4 ประตู ถ้านาย ก. และ ข.
จะเดินเข้าและออกห้องประชุม ได้กี่วิธีเมื่อ (ก.และ ข.ไม่ได้เดินไปด้วยกัน)
6.1 ทั้งสองจะเข้าและออกประตูใดก็ได้
6.2 แต่ละคนเข้าประตูใด จะออกประตูนั้นไม่ได้
6.3 ทั้งสองจะใช้วิธีการเข้าและออกเหมือนกันไม่ได้
ข้อ7.
สร้างจำนวน 4 หลัก แต่หลักใช้เลขซ้ำกันไม่ได้ โดยใช้เลข 0 ถึง 9
ให้เป็นจำนวนคี่ ระหว่าง 2,000 - 6,000 จะสร้างได้กี่จำนวน
100Years 27/07/51 20:37
แหม่..มาถึงก็ซัดเลย ไม่พูดพร่ำทำเพลงกันก่อนเลยแฮะ.. 5555
โจทย์เหล่านี้หาแนวคิดที่หลากหลายได้ยากครับ เพราะมันเป็นพื้นฐาน
และแทบทุกคนก็จะมองได้เพียงแง่เดียวแบบเดียว (หรือไม่ก็คล้ายกัน)
เหมือนกับว่า จะให้หาคำตอบของ 2+3 โดยให้แสดงวิธีทำหลายๆ วิธี.. มันก็ยากครับ :P
หลักการพื้นฐานของการนับ ก็คือ ถ้าเรามีงานหลายขั้นตอนที่ต้องทำต่อเนื่องจนครบ
จำนวนแบบที่สามารถทำได้ จะเท่ากับผลคูณของจำนวนทางเลือกในแต่ละขั้นตอนย่อยๆ
..เช่น มีเสื้อ 3 ตัว กางเกง 4 ตัว รองเท้า 2 คู่
เราจะเลือกเสื้อ กางเกง และรองเท้า มาใส่ให้ครบทั้งสามอย่าง ได้ทั้งหมด 3x4x2 = 24 แบบ
ถามว่ามาได้ยังไง มันมองได้แง่เดียวเท่านั้นครับ ก็คือมันเป็นจำนวนกิ่งของแผนภาพต้นไม้
ลองดูรูปในหนังสือเรียน หรือใน Math E-Book หัวข้อแรกของบทนี้ประกอบนะครับ..
===================================
ข้อ 4. ง่ายสุด ทำข้อ 4. ก่อนละกันครับ ... เราต้องทำงาน 4 ขั้นตอน (คือ หยอดๆๆ และหยอด)
แต่ละขั้นตอนเรามีทางเลือก (หยอดตู้ไหนดี?) ได้ 3 ทาง ดังนั้นคำตอบคือ 3x3x3x3 วิธี
ข้อ 5. มีการทำงาน 7 ขั้นตอน คือเลือกว่าแต่ละที่ ใครจะมานั่ง
เราควรเลือกที่คนขับก่อนครับเพราะว่ามีเงื่อนไข (ว่าคนขับไม่เป็นห้ามนั่งตรงนี้)
จะเลือกได้ 4 แบบ จากนั้นที่ต่อไปเลือกได้ 6, 5, 4, 3, 2, 1 แบบ ตามลำดับ
(จำนวนทางเลือกจะค่อยๆ ลดลงครับ ตามจำนวนคนที่เหลือที่ยังไม่ได้เข้าไปนั่งนั่นเอง)
คำตอบจึงเป็น 4x6x5x4x3x2x1 แบบ
หรือถ้าชอบเขียนสั้นๆ ก็เป็น 4x6! (แต่เวลาคิดเลขก็ต้องกระจายมันออกมาอยู่ดีครับ)
ข้อ 1. บ้างครับ ..จำนวน 5 หลัก เป็นจำนวนคู่ ก็แสดงว่าหลักหน่วยต้องเป็นเลขคู่
เราก็เลือกหลักหน่วยก่อนเลยดีกว่า (หลักอื่นๆ เป็นเลขอะไรก็ได้ ในบรรดา 1-9)
ซึ่งเลือกเลขที่จะมาวางในหลักหน่วยได้ 4 วิธี (2,4,6,8)
..จากนั้นเลือกสี่หลักที่เหลือ (หลักไหนก่อนก็ได้..) ได้ 9, 9, 9 วิธี
คำตอบจึงเป็น 4x9x9x9 แบบ (หรือ จำนวน นั่นแหละครับ)
[ แต่ถ้าห้ามใช้เลขซ้ำกัน จะต้องได้ 4x8x7x6 จำนวน ]
ข้อ 2. กับ 3. นั้น มีเลข 0 โผล่มาก่อกวนด้วย จะยากขึ้นนิดนึงเพราะหลักหน้าสุดห้ามเป็น 0
ข้อ 3. เลือกหลักหน่วย, พัน, ร้อย, สิบ ตามลำดับ จะได้คำตอบเป็น 3x3x4x3 จำนวน
ข้อ 2. ต้องแยกกรณีครับ เพราะการที่หลักหน่วยเป็น 0 หรือไม่เป็น 0 นั้นมีผลต่อหลักพัน
- กรณีหลักหน่วยเป็น 0 จะเลือกหลักหน่วย, พัน, ร้อย, สิบ ได้เท่ากับ 1x5x4x3 = 60 จำนวน
- กรณีหลักหน่วยไม่เป็น 0 จะเลือกได้เท่ากับ 2x4x4x3 = 96 จำนวน
แล้วเอามารวมกันได้คำตอบเป็น 156 จำนวนครับ (เมื่อแยกกรณี จะต้องเอามาบวกกันเสมอ)
ข้อที่เหลือขอตอบเลยนะ..
ข้อ 6.1 ตอบ (4x4)x(4x4) วิธี
ข้อ 6.2 ตอบ (4x3)x(4x3) วิธี
ข้อ 6.3 ตอบ 4x3x2x1 วิธี
ข้อ 7. แยกกรณี หลักหน่วยเป็น 3,5 กับกรณีหลักหน่วยเป็น 1,7,9 ..เพราะจะมีผลต่อหลักพัน
เลือกหลักหน่วย, พัน, ร้อย, สิบ ตามลำดับ.. และได้คำตอบ (2x3x8x7) + (3x4x8x7) จำนวน
ถ้าสงสัยสามารถโพสต์ถามในกระทู้นี้ต่อได้เลยครับ แล้วจะมาอธิบายย้อนให้ครับ..
โจทย์เหล่านี้หาแนวคิดที่หลากหลายได้ยากครับ เพราะมันเป็นพื้นฐาน
และแทบทุกคนก็จะมองได้เพียงแง่เดียวแบบเดียว (หรือไม่ก็คล้ายกัน)
เหมือนกับว่า จะให้หาคำตอบของ 2+3 โดยให้แสดงวิธีทำหลายๆ วิธี.. มันก็ยากครับ :P
หลักการพื้นฐานของการนับ ก็คือ ถ้าเรามีงานหลายขั้นตอนที่ต้องทำต่อเนื่องจนครบ
จำนวนแบบที่สามารถทำได้ จะเท่ากับผลคูณของจำนวนทางเลือกในแต่ละขั้นตอนย่อยๆ
..เช่น มีเสื้อ 3 ตัว กางเกง 4 ตัว รองเท้า 2 คู่
เราจะเลือกเสื้อ กางเกง และรองเท้า มาใส่ให้ครบทั้งสามอย่าง ได้ทั้งหมด 3x4x2 = 24 แบบ
ถามว่ามาได้ยังไง มันมองได้แง่เดียวเท่านั้นครับ ก็คือมันเป็นจำนวนกิ่งของแผนภาพต้นไม้
ลองดูรูปในหนังสือเรียน หรือใน Math E-Book หัวข้อแรกของบทนี้ประกอบนะครับ..
===================================
ข้อ 4. ง่ายสุด ทำข้อ 4. ก่อนละกันครับ ... เราต้องทำงาน 4 ขั้นตอน (คือ หยอดๆๆ และหยอด)
แต่ละขั้นตอนเรามีทางเลือก (หยอดตู้ไหนดี?) ได้ 3 ทาง ดังนั้นคำตอบคือ 3x3x3x3 วิธี
ข้อ 5. มีการทำงาน 7 ขั้นตอน คือเลือกว่าแต่ละที่ ใครจะมานั่ง
เราควรเลือกที่คนขับก่อนครับเพราะว่ามีเงื่อนไข (ว่าคนขับไม่เป็นห้ามนั่งตรงนี้)
จะเลือกได้ 4 แบบ จากนั้นที่ต่อไปเลือกได้ 6, 5, 4, 3, 2, 1 แบบ ตามลำดับ
(จำนวนทางเลือกจะค่อยๆ ลดลงครับ ตามจำนวนคนที่เหลือที่ยังไม่ได้เข้าไปนั่งนั่นเอง)
คำตอบจึงเป็น 4x6x5x4x3x2x1 แบบ
หรือถ้าชอบเขียนสั้นๆ ก็เป็น 4x6! (แต่เวลาคิดเลขก็ต้องกระจายมันออกมาอยู่ดีครับ)
ข้อ 1. บ้างครับ ..จำนวน 5 หลัก เป็นจำนวนคู่ ก็แสดงว่าหลักหน่วยต้องเป็นเลขคู่
เราก็เลือกหลักหน่วยก่อนเลยดีกว่า (หลักอื่นๆ เป็นเลขอะไรก็ได้ ในบรรดา 1-9)
ซึ่งเลือกเลขที่จะมาวางในหลักหน่วยได้ 4 วิธี (2,4,6,8)
..จากนั้นเลือกสี่หลักที่เหลือ (หลักไหนก่อนก็ได้..) ได้ 9, 9, 9 วิธี
คำตอบจึงเป็น 4x9x9x9 แบบ (หรือ จำนวน นั่นแหละครับ)
[ แต่ถ้าห้ามใช้เลขซ้ำกัน จะต้องได้ 4x8x7x6 จำนวน ]
ข้อ 2. กับ 3. นั้น มีเลข 0 โผล่มาก่อกวนด้วย จะยากขึ้นนิดนึงเพราะหลักหน้าสุดห้ามเป็น 0
ข้อ 3. เลือกหลักหน่วย, พัน, ร้อย, สิบ ตามลำดับ จะได้คำตอบเป็น 3x3x4x3 จำนวน
ข้อ 2. ต้องแยกกรณีครับ เพราะการที่หลักหน่วยเป็น 0 หรือไม่เป็น 0 นั้นมีผลต่อหลักพัน
- กรณีหลักหน่วยเป็น 0 จะเลือกหลักหน่วย, พัน, ร้อย, สิบ ได้เท่ากับ 1x5x4x3 = 60 จำนวน
- กรณีหลักหน่วยไม่เป็น 0 จะเลือกได้เท่ากับ 2x4x4x3 = 96 จำนวน
แล้วเอามารวมกันได้คำตอบเป็น 156 จำนวนครับ (เมื่อแยกกรณี จะต้องเอามาบวกกันเสมอ)
ข้อที่เหลือขอตอบเลยนะ..
ข้อ 6.1 ตอบ (4x4)x(4x4) วิธี
ข้อ 6.2 ตอบ (4x3)x(4x3) วิธี
ข้อ 6.3 ตอบ 4x3x2x1 วิธี
ข้อ 7. แยกกรณี หลักหน่วยเป็น 3,5 กับกรณีหลักหน่วยเป็น 1,7,9 ..เพราะจะมีผลต่อหลักพัน
เลือกหลักหน่วย, พัน, ร้อย, สิบ ตามลำดับ.. และได้คำตอบ (2x3x8x7) + (3x4x8x7) จำนวน
ถ้าสงสัยสามารถโพสต์ถามในกระทู้นี้ต่อได้เลยครับ แล้วจะมาอธิบายย้อนให้ครับ..
นวย 05/08/51 00:46 [ 1 ]
ขอบคุณมากๆครับพี่ที่ช่วยตอบให้
แต่ผมยังมีข้อสงสัยอีกเยอะมากๆเกี่ยวกับเรื่องนี้
เพราะเวลาเจอโจทย์ไปถามเพื่อน แต่ละคนคิดไม่เหมือนกันเลย
(แม้แต่เวลาอาจารย์เฉลย ผมยังไม่ค่อยจะมั่นใจเท่าไรเลย==)
เพราะเรื่องนี้มันหาวิธีตรวจสอบคำตอบยากมากๆ จะให้นั่งเขียนคำตอบออกมา
ทั้งหมดมันก็คงใช้เวลานานแน่ๆ
ร่ายมาซะยาวขอถามคำถามอีกนะครับ
1.ทอดลูกเต๋า 2 ลูกพร้อมๆกัน จงหาจำนวนวิธีที่จะได้ผลลัพธ์เหล่านี้
1.1 ผลรวมของแต้มเท่ากับสิบ
1.2 จำนวนแต้มต่างกัน
2.ทอดลูกเต๋า 2 ทีละลูก จงหาจำนวนวิธีที่จะได้ผลลัพธ์เหล่านี้
2.1 ผลรวมของแต้มเท่ากับสิบ
2.2 จำนวนแต้มต่างกัน
(ผมสงสัยลูกเต๋ามากเลยครับช่วยอธิบายทีครับ มันไม่น่ายาก
แต่ทำไมเพื่อนๆในห้องคิดออกมาคนละอย่างกันเลยครับ-*-)
3.มีชาย 2 คน มีประตู 6 ประตู
จงหาจำนวนวิธี เข้า-ออก โดยจะใช้วิธีเหมือนกันไม่ได้ (เข้า-ออกประตูซ้ำกันได้)
(** อันนี้เป็นข้อสอบย่อย ผมเจอผมทำไม่ได้เลยครับ)
4.มีของขวัญ 3 ชิ้น แจกให้เด็ก 6 คน ซึ่งทุกคนมีสิทธิ์รับได้ทั้ง 3 ชิ้น
จะแจกได้กี่วิธี
(โอ้ย! งง )
5.มีลูกดอก 3 ลูก มีเป้าอยู่ 5 ช่อง จะปาลูกดอกได้กี่วิธี
6.การเล่นทายผลฟุตบอล ถ้าชนะจะได้เงิน 1 บาท นาย ก. มีเงิน 1 บาท
เขาจะเลิกเล่นเมื่อเล่นครบ 5 ครั้ง หรือ เมื่อเงินหมด หรือ ได้เล่นชนะ 3 ครั้ง
(มีเงิน 4 บาท) ผลการเล่นมีแค่ได้กับเสีย จงหาวิธีการเล่นทั้งหมด
(ข้อนี้ผมคิดแบบยุ่งเหยิงมากๆ ขอวิธีคิดด้วยนะครับ)
ขอบคุณครับผม แล้วจะหาคำถามมาถามเรื่อยๆ นะคร้าบ...
แต่ผมยังมีข้อสงสัยอีกเยอะมากๆเกี่ยวกับเรื่องนี้
เพราะเวลาเจอโจทย์ไปถามเพื่อน แต่ละคนคิดไม่เหมือนกันเลย
(แม้แต่เวลาอาจารย์เฉลย ผมยังไม่ค่อยจะมั่นใจเท่าไรเลย==)
เพราะเรื่องนี้มันหาวิธีตรวจสอบคำตอบยากมากๆ จะให้นั่งเขียนคำตอบออกมา
ทั้งหมดมันก็คงใช้เวลานานแน่ๆ
ร่ายมาซะยาวขอถามคำถามอีกนะครับ
1.ทอดลูกเต๋า 2 ลูกพร้อมๆกัน จงหาจำนวนวิธีที่จะได้ผลลัพธ์เหล่านี้
1.1 ผลรวมของแต้มเท่ากับสิบ
1.2 จำนวนแต้มต่างกัน
2.ทอดลูกเต๋า 2 ทีละลูก จงหาจำนวนวิธีที่จะได้ผลลัพธ์เหล่านี้
2.1 ผลรวมของแต้มเท่ากับสิบ
2.2 จำนวนแต้มต่างกัน
(ผมสงสัยลูกเต๋ามากเลยครับช่วยอธิบายทีครับ มันไม่น่ายาก
แต่ทำไมเพื่อนๆในห้องคิดออกมาคนละอย่างกันเลยครับ-*-)
3.มีชาย 2 คน มีประตู 6 ประตู
จงหาจำนวนวิธี เข้า-ออก โดยจะใช้วิธีเหมือนกันไม่ได้ (เข้า-ออกประตูซ้ำกันได้)
(** อันนี้เป็นข้อสอบย่อย ผมเจอผมทำไม่ได้เลยครับ)
4.มีของขวัญ 3 ชิ้น แจกให้เด็ก 6 คน ซึ่งทุกคนมีสิทธิ์รับได้ทั้ง 3 ชิ้น
จะแจกได้กี่วิธี
(โอ้ย! งง )
5.มีลูกดอก 3 ลูก มีเป้าอยู่ 5 ช่อง จะปาลูกดอกได้กี่วิธี
6.การเล่นทายผลฟุตบอล ถ้าชนะจะได้เงิน 1 บาท นาย ก. มีเงิน 1 บาท
เขาจะเลิกเล่นเมื่อเล่นครบ 5 ครั้ง หรือ เมื่อเงินหมด หรือ ได้เล่นชนะ 3 ครั้ง
(มีเงิน 4 บาท) ผลการเล่นมีแค่ได้กับเสีย จงหาวิธีการเล่นทั้งหมด
(ข้อนี้ผมคิดแบบยุ่งเหยิงมากๆ ขอวิธีคิดด้วยนะครับ)
ขอบคุณครับผม แล้วจะหาคำถามมาถามเรื่อยๆ นะคร้าบ...
100Years 09/08/51 18:15 [ 2 ]
โดยทั่วไปถือว่าลูกเต๋าสองลูกต่างกันครับ ..นั่นคือ (1,2) จะต่างกับ (2,1)
ดังนั้นการโยนลูกเต๋า 2 ลูก จะมีผลที่เป็นไปได้ 6x6 = 36 แบบ
ได้แก่ (1,1), (1,2), (1,3), ..., (1,6), (2,1), (2,2), ... เรื่อยไปจนถึง (6,6)
แต่พี่นวยเห็นโจทย์ข้อ 1. กับ 2. ต่างกันแค่ทอดลูกเต๋าพร้อมหรือไม่พร้อมกัน
ก็ขอสรุปว่าในข้อ 2. ซึ่งทอดไม่พร้อมกัน มีลำดับก่อนหลัง หมายถึง 36 แบบ ..ชัวร์!
ข้อ 2.1 ถ้าพูดถึงผลบวกผลคูณของเต้มลูกเต๋า มักจะต้องนั่งไล่เอาครับ
ผลบวกเป็น 10 ก็ได้แก่ (4,6), (5,5), และ (6,4) ..ดังนั้นคำตอบคือ 3 วิธี
ข้อ 2.2 อันนี้ไม่ต้องนั่งไล่ครับ เพราะใช้กฎการนับได้
- แง่ที่ 1 คิดโดยตรง.. ลูกแรกเป็นอะไรก็ได้ ได้ 6 วิธี
แล้วอีกลูกต้องออกแต้มไม่เหมือนลูกแรก ซึ่งจะได้ 5 วิธีเสมอ
ดังนั้นตอบ 6x5 = 30 วิธี ครับ
- แง่ที่ 2 ลบออก (พี่นวยจะชอบวิธีนี้มากกว่า เพราะคิดสั้นดี)
เอาวิธีทั้งหมดคือ 6x6 = 36 ลบออกด้วยวิธีที่เขาไม่ได้ถาม
นั่นคือออกแต้มเหมือนกัน = 6 แบบ (1,1), (2,2), (3,3), ... (6,6)
ก็จะคิดได้คำตอบเป็น 30 วิธีเช่นกันครับ
ส่วนข้อ 1. โจทย์กำกวมครับ ถึงแม้จะทอดสองลูกพร้อมกันเลย ก็จะคิดไปได้ 2 ทาง
คือถ้าลูกเต๋าต่างกัน (เช่น ลูกเต๋าคนละสี หรือว่าเราจำได้ว่ามันต่างกันตรงไหน)
จะได้วิธีทั้งหมดเป็น 36 แบบ และจะตอบเช่นเดียวกับข้อ 2.1 และ 2.2 เลยครับ
แต่ถ้าโจทย์เขาต้องการให้ลูกเต๋าเหมือนกัน นั่นคือ (1,2) เป็นวิธีเดียวกับ (2,1)
(หมายความว่า โยนพร้อมกันแล้วก็จำไม่ได้ว่าลูกไหนเป็นลูกไหน)
จำนวนวิธีทั้งหมดจะมี 21 แบบครับ (ถ้าลองเขียนไล่ดูจะรู้ว่าทำไมถึงไม่ลดครึ่งนึง)
ถ้าเป็นแบบนี้ ข้อ 1.1 จะได้ (4,6), (5,5) รวม 2 วิธี
ข้อ 1.2 จะได้ 21 - 6 = 15 วิธี ครับ (ลบเอาง่ายสุด เพราะเรารู้จำนวนวิธีทั้งหมด)
ดังนั้นการโยนลูกเต๋า 2 ลูก จะมีผลที่เป็นไปได้ 6x6 = 36 แบบ
ได้แก่ (1,1), (1,2), (1,3), ..., (1,6), (2,1), (2,2), ... เรื่อยไปจนถึง (6,6)
แต่พี่นวยเห็นโจทย์ข้อ 1. กับ 2. ต่างกันแค่ทอดลูกเต๋าพร้อมหรือไม่พร้อมกัน
ก็ขอสรุปว่าในข้อ 2. ซึ่งทอดไม่พร้อมกัน มีลำดับก่อนหลัง หมายถึง 36 แบบ ..ชัวร์!
ข้อ 2.1 ถ้าพูดถึงผลบวกผลคูณของเต้มลูกเต๋า มักจะต้องนั่งไล่เอาครับ
ผลบวกเป็น 10 ก็ได้แก่ (4,6), (5,5), และ (6,4) ..ดังนั้นคำตอบคือ 3 วิธี
ข้อ 2.2 อันนี้ไม่ต้องนั่งไล่ครับ เพราะใช้กฎการนับได้
- แง่ที่ 1 คิดโดยตรง.. ลูกแรกเป็นอะไรก็ได้ ได้ 6 วิธี
แล้วอีกลูกต้องออกแต้มไม่เหมือนลูกแรก ซึ่งจะได้ 5 วิธีเสมอ
ดังนั้นตอบ 6x5 = 30 วิธี ครับ
- แง่ที่ 2 ลบออก (พี่นวยจะชอบวิธีนี้มากกว่า เพราะคิดสั้นดี)
เอาวิธีทั้งหมดคือ 6x6 = 36 ลบออกด้วยวิธีที่เขาไม่ได้ถาม
นั่นคือออกแต้มเหมือนกัน = 6 แบบ (1,1), (2,2), (3,3), ... (6,6)
ก็จะคิดได้คำตอบเป็น 30 วิธีเช่นกันครับ
ส่วนข้อ 1. โจทย์กำกวมครับ ถึงแม้จะทอดสองลูกพร้อมกันเลย ก็จะคิดไปได้ 2 ทาง
คือถ้าลูกเต๋าต่างกัน (เช่น ลูกเต๋าคนละสี หรือว่าเราจำได้ว่ามันต่างกันตรงไหน)
จะได้วิธีทั้งหมดเป็น 36 แบบ และจะตอบเช่นเดียวกับข้อ 2.1 และ 2.2 เลยครับ
แต่ถ้าโจทย์เขาต้องการให้ลูกเต๋าเหมือนกัน นั่นคือ (1,2) เป็นวิธีเดียวกับ (2,1)
(หมายความว่า โยนพร้อมกันแล้วก็จำไม่ได้ว่าลูกไหนเป็นลูกไหน)
จำนวนวิธีทั้งหมดจะมี 21 แบบครับ (ถ้าลองเขียนไล่ดูจะรู้ว่าทำไมถึงไม่ลดครึ่งนึง)
ถ้าเป็นแบบนี้ ข้อ 1.1 จะได้ (4,6), (5,5) รวม 2 วิธี
ข้อ 1.2 จะได้ 21 - 6 = 15 วิธี ครับ (ลบเอาง่ายสุด เพราะเรารู้จำนวนวิธีทั้งหมด)
นวย 10/08/51 23:36 [ 3 ]
ต่อไปข้อ 5. ก่อนครับ เพราะง่ายดี
ยังเป็นกฎการนับเบื้องต้นเหมือนโจทย์ข้อ 1. ถึง 7. ด้านบนอยู่
(ซึ่งมันจะพลิกแพลงวิธีคิดไม่ได้ เพราะมันมีแต่คูณกันดื้อๆ)
ในข้อนี้มีงาน 3 ขั้นตอน คือ ปา ปา และก็ปา..
โดยแต่ละขั้นมีหนทางที่เกิดขึ้นได้ 5 แบบ ดังนั้นคำตอบคือ 5x5x5 วิธี ครับ
หรือถ้าคำนึงถึงการปาไม่เข้าเป้าสักช่องเลยด้วย ก็จะได้คำตอบ 6x6x6 วิธี
..ถ้าให้พี่นวยเลือก จะตอบ 6x6x6 เพราะคิดว่าคนออกโจทย์ตั้งใจหลอกแน่ๆ
แบบข้อ 4. ก็ยังถือว่าเป็นโจทย์พื้นฐานอยู่นะครับ (ไม่พลิกแพลงอะไรเลย)
"ทุกคนมีสิทธิ์รับได้ทั้งสามชิ้น" ก็หมายความว่า แจกซ้ำคนเดิมได้ ไม่ห้าม..
งานที่เราต้องทำมี 3 ขั้นตอน ได้แก่ แจก แจก และแจก
โดยแต่ละขั้นตอนมีทางเลือก (แจกให้ใครดี?) ได้ 6 ทาง
คำตอบจึงเป็น 6x6x6 วิธี ครับ
(แต่ถ้าแต่ละคนรับได้แค่ชิ้นเดียว คำตอบจะเป็น 6x5x4 นะ)
ส่วนข้อ 3. ซับซ้อนขึ้นมาหน่อย แต่ก็ยังไม่พ้นหลักการนับอยู่ดีครับ
ถ้าเราพิจารณาคนๆ เดียว การเดินเข้า-ออก (ซ้ำประตูได้) จะมี 6x6 = 36 แบบ
แต่คนที่สองดันห้ามใช้วิธีเข้า-ออกให้เหมือนตาคนแรกนั่น..
โจทย์กำกวมอีกแล้วครับ เพราะตีความไปได้สองทาง คือ
(1) ห้ามเข้าประตูเดียวกันกับคนแรก และห้ามออกประตูเดียวกันกับคนแรก
อันนี้คนที่สองจะเหลือทางเลือกแค่ 5x5 = 25 แบบ
ดังนั้นคำตอบข้อนี้จะเป็น 36x25 วิธีครับ ..หรือคิดรวดเดียวเป็น (6x6)x(5x5) ก็ได้
(2) ถ้าตีความว่า ห้ามใช้ "วิธีเข้าออก" ที่ซ้ำกับคนแรก
(คือใช้ได้หมด ยกเว้น ทั้งเข้าทั้งออกเหมือนคนแรกเป๊ะทั้งสองอย่าง)
ลักษณะนี้จะได้คำตอบเป็น 36x35 วิธี ครับ
ยังเป็นกฎการนับเบื้องต้นเหมือนโจทย์ข้อ 1. ถึง 7. ด้านบนอยู่
(ซึ่งมันจะพลิกแพลงวิธีคิดไม่ได้ เพราะมันมีแต่คูณกันดื้อๆ)
ในข้อนี้มีงาน 3 ขั้นตอน คือ ปา ปา และก็ปา..
โดยแต่ละขั้นมีหนทางที่เกิดขึ้นได้ 5 แบบ ดังนั้นคำตอบคือ 5x5x5 วิธี ครับ
หรือถ้าคำนึงถึงการปาไม่เข้าเป้าสักช่องเลยด้วย ก็จะได้คำตอบ 6x6x6 วิธี
..ถ้าให้พี่นวยเลือก จะตอบ 6x6x6 เพราะคิดว่าคนออกโจทย์ตั้งใจหลอกแน่ๆ
แบบข้อ 4. ก็ยังถือว่าเป็นโจทย์พื้นฐานอยู่นะครับ (ไม่พลิกแพลงอะไรเลย)
"ทุกคนมีสิทธิ์รับได้ทั้งสามชิ้น" ก็หมายความว่า แจกซ้ำคนเดิมได้ ไม่ห้าม..
งานที่เราต้องทำมี 3 ขั้นตอน ได้แก่ แจก แจก และแจก
โดยแต่ละขั้นตอนมีทางเลือก (แจกให้ใครดี?) ได้ 6 ทาง
คำตอบจึงเป็น 6x6x6 วิธี ครับ
(แต่ถ้าแต่ละคนรับได้แค่ชิ้นเดียว คำตอบจะเป็น 6x5x4 นะ)
ส่วนข้อ 3. ซับซ้อนขึ้นมาหน่อย แต่ก็ยังไม่พ้นหลักการนับอยู่ดีครับ
ถ้าเราพิจารณาคนๆ เดียว การเดินเข้า-ออก (ซ้ำประตูได้) จะมี 6x6 = 36 แบบ
แต่คนที่สองดันห้ามใช้วิธีเข้า-ออกให้เหมือนตาคนแรกนั่น..
โจทย์กำกวมอีกแล้วครับ เพราะตีความไปได้สองทาง คือ
(1) ห้ามเข้าประตูเดียวกันกับคนแรก และห้ามออกประตูเดียวกันกับคนแรก
อันนี้คนที่สองจะเหลือทางเลือกแค่ 5x5 = 25 แบบ
ดังนั้นคำตอบข้อนี้จะเป็น 36x25 วิธีครับ ..หรือคิดรวดเดียวเป็น (6x6)x(5x5) ก็ได้
(2) ถ้าตีความว่า ห้ามใช้ "วิธีเข้าออก" ที่ซ้ำกับคนแรก
(คือใช้ได้หมด ยกเว้น ทั้งเข้าทั้งออกเหมือนคนแรกเป๊ะทั้งสองอย่าง)
ลักษณะนี้จะได้คำตอบเป็น 36x35 วิธี ครับ
นวย 10/08/51 23:49 [ 4 ]
สุดท้ายข้อ 6. ครับ เป็นโจทย์ที่เรียกว่า "ไร้กระบวนท่า"
เพราะว่าจำนวนขั้นตอนที่เราต้องทำเนี่ย ไม่ตายตัว แต่ขึ้นอยู่กับผลที่ออกด้วย..
สถานการณ์แบบนี้เราต้องนั่งไล่นับอีกแล้วครับ (เขียนแจงออกมาให้ครบทุกทาง)
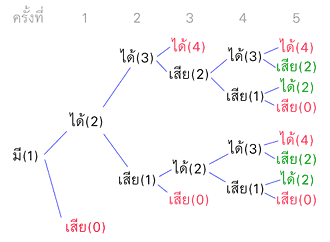
สีแดงคือหยุด จากเงื่อนไข "เงินหมด" หรือ "ชนะ 3 ครั้ง (มีเงิน 4 บาท)"
ส่วนสีเขียวก็คือหยุดเช่นกัน เพราะเงื่อนไข "เล่นครบ 5 ครั้ง"
ดังนั้น จากการนับในรูป จะพบว่าจำนวนแบบที่เกิดขึ้นได้ มีอยู่ 11 แบบครับ
ได้แก่.. (ได้,ได้,ได้),
(ได้,ได้,เสีย,ได้,ได้), (ได้,ได้,เสีย,ได้,เสีย),
(ได้,ได้,เสีย,เสีย,ได้), (ได้,ได้,เสีย,เสีย,เสีย),
(ได้,เสีย,ได้,ได้,ได้), (ได้,เสีย,ได้,ได้,เสีย),
(ได้,เสีย,ได้,เสีย,ได้), (ได้,เสีย,ได้,เสีย,เสีย),
(ได้,เสีย,เสีย), (เสีย)
โอย.. เพลียเลย แหะๆๆ ขอตัวไปนอนละครับวันนี้.. :P
เพราะว่าจำนวนขั้นตอนที่เราต้องทำเนี่ย ไม่ตายตัว แต่ขึ้นอยู่กับผลที่ออกด้วย..
สถานการณ์แบบนี้เราต้องนั่งไล่นับอีกแล้วครับ (เขียนแจงออกมาให้ครบทุกทาง)

สีแดงคือหยุด จากเงื่อนไข "เงินหมด" หรือ "ชนะ 3 ครั้ง (มีเงิน 4 บาท)"
ส่วนสีเขียวก็คือหยุดเช่นกัน เพราะเงื่อนไข "เล่นครบ 5 ครั้ง"
ดังนั้น จากการนับในรูป จะพบว่าจำนวนแบบที่เกิดขึ้นได้ มีอยู่ 11 แบบครับ
ได้แก่.. (ได้,ได้,ได้),
(ได้,ได้,เสีย,ได้,ได้), (ได้,ได้,เสีย,ได้,เสีย),
(ได้,ได้,เสีย,เสีย,ได้), (ได้,ได้,เสีย,เสีย,เสีย),
(ได้,เสีย,ได้,ได้,ได้), (ได้,เสีย,ได้,ได้,เสีย),
(ได้,เสีย,ได้,เสีย,ได้), (ได้,เสีย,ได้,เสีย,เสีย),
(ได้,เสีย,เสีย), (เสีย)
โอย.. เพลียเลย แหะๆๆ ขอตัวไปนอนละครับวันนี้.. :P
นวย 11/08/51 00:00 [ 5 ]
พี่คะ คือนู๋อยากทราบว่าหลักในการสร้างเลขโดดมียังงัยบ้างคะ
แล้วดูยังงัยว่าต้องใช้เป็นกรณี หรือขั้นตอน คะ
ขอถามโจทย์ข้อที่1 เรยคะ
ถ้าใช้ตัวเลข0,1,2,3,4มาสร้างเป็นเลขสี่หลัก โดยแต่ละหลัก ห้ามใช้เลขซ้ำกันจะสร้างได้กี่จำนวนถ้า
10.1ไม่มีเงื่อนไนใดๆ
(อันนี้นิ่มทำเป็นขั้นตอน ได้ 96 วิธี แต่เห็นในเน็ตมีทำเป็นกรณีแบบ หลักหน่อยเป็นศูนย์ กับ หลักหน่วยไม่เป็นศูนย์อะ แต่ได้คำตอบเท่ากัน)
10.2เลขที่สร้างต้องเป็นเลขจำนวนเต็มคี่(ข้อนี้ก็ทำเป็นแบบขั้นตอนได้ 36วิธี และทำเป็นกรณีได้ 36วิธีเท่ากันคะ)
10.3เลขที่สร้างต้องเป็นเลขจำนวนคู่ (ข้อนี้แหละคะ คือปัญหาที่ให้งง! ลองทำเป็นแบบ เริ่มจากหลักหน่วย 3*4*3*2=72วิธี แต่ทำเป็นกรณี ได้คำตอบไม่ตรงอะคะ ไม่แน่ใจว่าคิดเลขผิดรึป่าวคะ รึว่า มีหลักการยังงัยคะ)
*****รบกวนด้วยนะคะพี่*******
พี่คะ ในการสร้างเลขโดดแบบตัวอย่างต่อไปนี้
อันนี้เป็นของอาจารย์ยกตัวอย่างอะคะ ที่สงสัยคือทำไม่ทำเป็นขั้นตอนไม่ได้
ข้อที่2 ในการสร้างเลขโดยใช้เลขโดด1-7จะสร้างเลขที่มีค่าไม่เกิน 1000 ได้ทั้งหมดกี่จำนวน
วิธีทำ เริ่มทำที่1หลัก จนถึง3หลัก สี่หลักสร้างไม่ได้เพราะไม่มีเลขศูนย์ให้ใช้
กรณีที่1 หนึ่งหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
กรณีที่2 สองหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
เลือกเลขใส่หลักสิบได้ 7 วิธี
เพราะฉะนั้น 7*7=49 วิธี
กรณีที่3 สามหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
เลือกเลขใส่หลักสิบได้ 7 วิธี
เลือกเลขใส่หลักร้อยได้ 7 วิธี
เพราะฉะนั้น 7*7*7=343วิธี
ตอบ ได้เลขทั้งหมด 7+49+343=399จำนวน
แล้วดูยังงัยว่าต้องใช้เป็นกรณี หรือขั้นตอน คะ
ขอถามโจทย์ข้อที่1 เรยคะ
ถ้าใช้ตัวเลข0,1,2,3,4มาสร้างเป็นเลขสี่หลัก โดยแต่ละหลัก ห้ามใช้เลขซ้ำกันจะสร้างได้กี่จำนวนถ้า
10.1ไม่มีเงื่อนไนใดๆ
(อันนี้นิ่มทำเป็นขั้นตอน ได้ 96 วิธี แต่เห็นในเน็ตมีทำเป็นกรณีแบบ หลักหน่อยเป็นศูนย์ กับ หลักหน่วยไม่เป็นศูนย์อะ แต่ได้คำตอบเท่ากัน)
10.2เลขที่สร้างต้องเป็นเลขจำนวนเต็มคี่(ข้อนี้ก็ทำเป็นแบบขั้นตอนได้ 36วิธี และทำเป็นกรณีได้ 36วิธีเท่ากันคะ)
10.3เลขที่สร้างต้องเป็นเลขจำนวนคู่ (ข้อนี้แหละคะ คือปัญหาที่ให้งง! ลองทำเป็นแบบ เริ่มจากหลักหน่วย 3*4*3*2=72วิธี แต่ทำเป็นกรณี ได้คำตอบไม่ตรงอะคะ ไม่แน่ใจว่าคิดเลขผิดรึป่าวคะ รึว่า มีหลักการยังงัยคะ)
*****รบกวนด้วยนะคะพี่*******
พี่คะ ในการสร้างเลขโดดแบบตัวอย่างต่อไปนี้
อันนี้เป็นของอาจารย์ยกตัวอย่างอะคะ ที่สงสัยคือทำไม่ทำเป็นขั้นตอนไม่ได้
ข้อที่2 ในการสร้างเลขโดยใช้เลขโดด1-7จะสร้างเลขที่มีค่าไม่เกิน 1000 ได้ทั้งหมดกี่จำนวน
วิธีทำ เริ่มทำที่1หลัก จนถึง3หลัก สี่หลักสร้างไม่ได้เพราะไม่มีเลขศูนย์ให้ใช้
กรณีที่1 หนึ่งหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
กรณีที่2 สองหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
เลือกเลขใส่หลักสิบได้ 7 วิธี
เพราะฉะนั้น 7*7=49 วิธี
กรณีที่3 สามหลัก
เลือกเลขใส่หลักหน่วยได้ 7 วิธี
เลือกเลขใส่หลักสิบได้ 7 วิธี
เลือกเลขใส่หลักร้อยได้ 7 วิธี
เพราะฉะนั้น 7*7*7=343วิธี
ตอบ ได้เลขทั้งหมด 7+49+343=399จำนวน
น้องนิ่ม 22/12/54 17:19 [ 6 ]