ช่วยอธิบายวิธีคิดหาพจน์ทั่วไปเกี่ยวกับเลขลำดับนี้หน่อยครับตอบ: 6, อ่าน: 20672, แท็ก: ถามโจทย์, ลำดับ

เนื่องจากลำดับนี้ไม่ใช่ลำดับเลขคณิต และไม่ใช่ลำดับเรขาคณิต
เราจึงเริ่มด้วยวิธียอดฮิต นั่นคือลองหาผลต่างของแต่ละพจน์ที่อยู่ติดกันดูครับ
แล้วก็พบว่าเมื่อหาผลต่าง ซ้ำๆ ไปจนถึงรอบที่ 3 จะได้ผลต่างเป็นค่าคงตัว



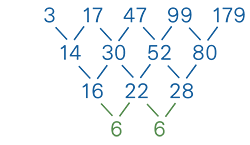
แสดงว่าลำดับนี้เป็นลำดับในรูป "พหุนามดีกรีสาม" หรือ $a_n = A n^3 + B n^2 + C n + D$
หน้าที่ของเราก็คือหาค่าสัมประสิทธิ์ A, B, C, D ออกมาให้ครบทั้งสี่ตัวก็เป็นอันเสร็จ
การหาก็ทำได้โดยแทนค่าพจน์ต่างๆ ลงไป 4 แบบ (เพื่อให้ได้ 4 สมการนั่นเอง)

พจน์ที่ 1 : $a_1 = A + B + C + D = 3$
พจน์ที่ 2 : $a_2 = 8A + 4B + 2C + D = 17$
พจน์ที่ 3 : $a_3 = 27A + 9B + 3C + D = 47$
พจน์ที่ 4 : $a_4 = 64A + 16B + 4C + D = 99$

จากนั้นก็นั่งแก้ระบบสมการตามอัธยาศัย ก็จะทราบค่า A, B, C, D ครับ

===========================================

แต่เดี๋ยวก่อน! แก้ 4 สมการ 4 ตัวแปร ดูไม่น่าทำเลยเนอะ
ลองเทคนิค "ใช้พจน์ที่ 0" สิครับ สะดวกกว่าเยอะ (เพราะ n=0 ทำให้คิดเลขง่าย)
ซึ่งพจน์ที่ 0 ก็หาได้ดังรูป.. (คิดย้อนขึ้นมาจาก 6, 10, 4, จนทราบพจน์ที่ 0 เป็น -1)



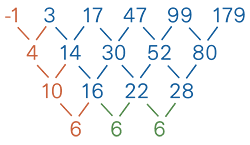
ดังนั้นสมการก็คือ $a_0 = 0A + 0B + 0C + D = -1$
พจน์ที่ 0 จะทำให้เรารู้ค่า D ว่าเป็น -1 เลยทันทีครับ!
เราจึงติดแค่ A, B, C ..ก็ยกมาแก้แค่ 3 สมการแบบนี้ก็พอ

พจน์ที่ 1 : $a_1 = A + B + C - 1 = 3$
พจน์ที่ 2 : $a_2 = 8A + 4B + 2C - 1 = 17$
พจน์ที่ 3 : $a_3 = 27A + 9B + 3C - 1 = 47$

สรุปแล้วจะได้ค่า A, B, C เป็น 1, 2, 1 ตามลำดับ
และคำตอบ (รูปทั่วไปของลำดับ) ก็คือ $a_n = n^3 + 2 n^2 + n - 1$ นั่นเองครับ

ขออธิบายเพิ่มเติมให้ครอบคลุมยิ่งขึ้นนะครับ
- ถ้าหาผลต่างรอบแรกได้ค่าคงตัวเลยทันที จะเป็นพหุนามดีกรีหนึ่ง (ลำดับเลขคณิต)
- ถ้าหาผลต่างจนถึงรอบที่สองแล้วได้ค่าคงตัว จะเป็นพหุนามดีกรีสอง
- และเป็นเช่นนี้ไปเรื่อยๆ ไม่ว่ากำลังของพหุนามจะมากเท่าใด
ซึ่งในโจทย์นี้หาผลต่างจนถึงรอบที่สามแล้วได้ค่าคงตัว จึงเป็นพหุนามดีกรีสามครับ

ทีนี้ถ้าไม่หาผลต่างล่ะ จะมีวิธีคิดแบบอื่นไหม?
..ก็มีครับ คือค่อยๆ บิด ค่อยๆ แปลง ให้กลายเป็นลำดับที่สวยขึ้น (และเรารู้รูปทั่วไป)
แต่วิธีแบบนี้มันไร้กระบวนท่า เดี๋ยวจะกลายเป็นทดสอบเชาวน์ไปซะก่อน จึงไม่แนะนำครับ

จากโจทย์.. a_n คือลำดับ 3, 17, 47, 99, 179, ...
เราเห็นว่าเป็นเลขคี่ เลยลองบวก 1 ดูหน่อยดีกว่า (ห้ามถามว่าทำไม..*)
ก็จะได้ a_n+1 คือลำดับ 4, 18, 48, 100, 180, ...
จากนั้นก็สังเกตอีกแล้วว่าแต่ละพจน์หาร n (1, 2, 3, ...) ลงตัว (ห้ามถามว่ารู้ได้ไง..*)
จะได้ (a_n+1) / n คือลำดับ 4, 9, 16, 25, 36, ...
ซึ่งผลที่ได้ในขณะนี้ แต่ละพจน์ก็คือกำลังสองของจำนวนนับนั่นเอง (โดยเริ่มจาก 2², 3², ...)

ก็จะสรุปสมการได้ดังนี้ครับ.. (a_n+1) / n = (n+1)²
ย้ายข้าง ได้คำตอบเป็น a_n = n (n+1)² - 1

หมายเหตุ
1. เมื่อแจกแจงพหุนามออกมา ก็จะเหมือนกับที่คิดไว้ด้วยวิธีข้างบนนั่นแหละครับ
* 2. ที่ห้ามถามว่ารู้ได้ไง ก็เพราะมันบอกไม่ได้ครับ วิธีการแต่ละข้อมันไม่ตายตัว
ดังนั้นควรพยายามมองให้เป็นวิธีข้างบนนู้น จะดูเป็นเหตุเป็นผลมากกว่าครับ..

ได้เสมอครับ ถ้าเป็น polynomial นะ
อธิบายง่ายๆ ว่า ดิฟกี่ครั้งแล้วได้ค่าคงที่ ก็จะมีดีกรีเท่านั้น

===========================================

ขอเสริมอีกนิด..
สำหรับลำดับที่บอกจำนวนพจน์มาไม่มาก และไม่รู้จะหารูปทั่วไปยังไงแล้ว
หากเราหาผลต่างไปเรื่อยๆ ไม่กี่รอบมันก็จะเหลือเลขแค่ตัวเดียว (ในที่สุด)
จึงทำให้เราโมเมได้ว่า "ชั้นนี้เป็นค่าคงที่"
แล้วหาคำตอบในรูป polynomial ได้ตลอดศกเลยเชียวล่ะคร้าบ.. :P

เพราะฉะนั้น โจทย์ในรูปแบบที่ไม่ใช่ลำดับเลขคณิต หรือเรขาคณิต
(หรืออื่นๆ ที่มีชื่อเรียกเฉพาะให้เข้าใจตรงกัน) จะไม่นิยมถามรูปทั่วไป หรือถามพจน์ถัดไป
เพราะว่ามันตอบได้หลากหลายแบบจ่ะ