Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0438 จาก 0508
| กระทู้ที่ 0437 บทความ#1 : นาย A กับนาย B | ตั้งกระทู้ใหม่ | กระทู้ที่ 0439 บทความ#3 : จะไปเป็นดาวโดดเด่น.. ได้ยังไง! |
บทความ#2 : n เหลี่ยมแนบในวงกลมตอบ: 1, อ่าน: 27528
มาถึงเรื่องที่คราวก่อนตั้งใจจะเล่าแล้วครับ มัวไปพูดเรื่องอื่นอยู่ตั้งนาน (แต่นั่นก็เป็นเรื่องสำคัญนะ) สงสัยถ้าน้ำยังท่วมอยู่ ผมคงได้มานั่งเขียนอีกหลายตอนเลยครับ ^ ^
จากที่ได้เกริ่นไปแล้วว่าผมไม่ได้เป็นคนที่ชอบคิดเลขเป็นชีวิตจิตใจ แถมยังพยายามไม่คิดถ้าไม่จำเป็นอีกต่างหาก (แต่เรื่องที่ผมมองว่าจำเป็นอาจจะมีเยอะก็ได้นะครับ อิๆ) ดังนั้นนอกจากเวลาที่สอนพิเศษและเวลาทำหนังสือแล้ว โอกาสจะได้ใช้ความรู้ระดับ ม.ปลาย ในชีวิตจริงนั้นมีน้อยเหลือเกิน ที่ทำบ่อยก็แค่บวกลบคูณหารแบบประถมเวลาจะซื้อของ เหมือนกับทุกคนนั่นแหละครับ
เมื่อหลายวันก่อน เพื่อนผมอีกคนหนึ่งที่ทำงานเป็นโปรดิวเซอร์อัลบั้มเพลง (และเป็นคนที่มีความคิดและมุมมองก้าวล้ำไปไกลกว่าเพื่อนร่วมรุ่นมาตลอด) ได้ส่งโจทย์ข้อหนึ่งมาให้ผมใช้ความรู้ทางคณิตศาสตร์ช่วยแก้ให้ ที่จริงมันเป็นโมเดลเกี่ยวกับการเดินทางสะท้อนของเสียงภายในหน้าตัดวงกลม ซึ่งเขาบอกว่าเกิดนิมิตขึ้นขณะเคลิ้มๆ กึ่งหลับกึ่งตื่นครับ
ผมดูโจทย์ข้อนี้ในมุมคณิตศาสตร์แล้ว มีทั้งแง่มุมน่ารัก ท้าทาย และไม่ยากเกิน ม.ปลาย (ถ้ายากผมก็ไม่คิดหรอกครับ ฮ่าๆๆ) ประจวบกับไม่ได้สอนพิเศษมาหลายเดือน จนบางเวลาสมองซีกซ้ายมันตื้อๆ ไม่ค่อยแล่น เลยตื่นเต้นรีบหยิบกระดาษขึ้นมาทดในทันที พอแก้จนเสร็จก็รู้สึกว่าได้ไอเดียใหม่ๆ จากงานนี้หลายอย่าง คิดว่าเอามาเขียนบทความดีกว่า อย่างน้อยที่สุดน้องๆ นักเรียนก็คงได้เห็นว่าเวลาเจอโจทย์แล้วจะค่อยๆ คิดจนจบได้ยังไง.. นะครับ ^ ^
เอาล่ะ มาดูโจทย์ที่ว่ากันดีกว่าครับ
=============================================
กำหนดวงกลม C มีรัศมี r และมีจุด P เป็นจุดหนึ่งบนเส้นรอบวง จากจุดนี้สามารถยิง (ลาก) เส้นตรงออกไปสะท้อนที่ผิววงกลมได้ แนวการเดินที่สนใจคือแนวที่สะท้อนจนกลับมาถึงจุด P เท่านั้น โดยจะสะท้อนกี่ครั้งก็ได้ (คุณผู้อ่านลองวาดรูปตามไปด้วยแล้วจะเห็นความสนุกครับ)
เช่น แนวเดินที่สั้นที่สุดคือการยิงผ่านจุดศูนย์กลาง จะสะท้อนขอบวงกลมฝั่งตรงข้ามแล้วย้อนกลับมาที่จุด P ในทันที สรุประยะทางได้เท่ากับ 4r และมุมที่ยิงออกไปเท่ากับ 90° (เทียบกับเส้นสัมผัส ณ จุด P)
เข้าสู่คำถามนะครับ
1. ถ้าสมมติยิงทำมุม 60° จะเกิดการสะท้อนสองครั้งแล้วกลับมาที่จุดเดิม เป็นรูปสามเหลี่ยมด้านเท่าพอดี หรือถ้ายิงทำมุม 45° จะเกิดรูปสี่เหลี่ยมจัตุรัส ฯลฯ เหล่านี้เรียกว่ากรณี "n เหลี่ยมด้านเท่า"
อยากให้หาสูตรคำนวณระยะทางการวิ่งจนครบรอบ เมื่อกำหนดค่า n ต่างๆ (ก็แสดงว่าถ้า n มีค่ามากขึ้นเรื่อยๆ คำตอบจะต้องเข้าใกล้เส้นรอบวง 2πr) และบอกด้วยว่ามุมที่ยิงในแต่ละรูปต้องมีค่าเท่าไร
2. ถ้ายิงทำมุม (คาดว่า) 72° จะเกิดการสะท้อนเป็นรูปดาวห้าแฉกแล้วจึงกลับจุดเดิมพอดี แบบนี้ถือเป็นกรณีที่เส้นทางเดินตัดกันเป็น "รูปดาวแฉกๆ"
คำถามคือ จะสรุปการเดินทางเป็นลักษณะต่างๆ ได้อย่างไรบ้าง และให้หาสูตรคำนวณระยะทาง กับมุมที่ยิงด้วยเหมือนข้อแรก
=============================================
วาดเสร็จแล้วดูเหมือนเป็นคำถามที่ยากนะครับ กรณีรูป n เหลี่ยมนี่ยังไม่เท่าไร ยังพอจะได้เห็นในข้อสอบกันบ้าง แต่กรณีดาวแฉกๆ มันเกินสิ่งที่เราคุ้นเคยไปแล้ว จินตนาการไปถึงยากจัง แล้วดาวมันก็มีได้ไม่รู้กี่ร้อยกี่พันแบบ.. แต่เมื่อผมคิดจนเสร็จ ก็พบว่ามันใช้ความรู้เสี้ยวเดียวของตรีโกณ (ม.5) เท่านั้นเองครับ! คือสามารถเอาไปออกข้อสอบเอ็นท์ได้เลย และเป็นข้อสอบประเภทที่ "ดูยาก แต่เฉลยกลับไม่ค่อยมีอะไร" อีกต่างหาก
ถ้าใครอยากทดสอบความรู้ที่มี โดยเฉพาะข้อ 1. ซึ่งควรจะคิดได้ทุกคน ก็ลองหยิบกระดาษปากกามาลุยก่อนเลยครับ การคิดได้เองไม่เหมือนรอฟังเฉลยนะครับ (ใครที่เรียนถึง ม.5 แล้ว แต่คิดข้อ 1. ไม่ได้ ควรพิจารณาตนเองด่วน!) ..ส่วนข้อ 2. ยากหน่อย แต่ถ้าใครคิดคำตอบได้ ก็จะเกิดพุทธิไอเดียเท่ากับที่ผมได้มาแล้วจากโจทย์นี้เช่นกันครับ ถือว่าคุ้มอย่างยิ่ง ^ ^
... หลังจากลองวาดรูปหรือทดเองแล้ว ก็มาดูขั้นตอนที่ผมคิดกันบ้างนะครับ ...
เริ่มจากข้อแรก ผมลองวาดวงกลมแล้วใส่ 3 เหลี่ยม, 4 เหลี่ยม, 5 เหลี่ยม ลงไปอย่างละรูป แล้วก็พบข้อมูลเบื้องต้นว่า ต้องเป็นแบบด้านเท่ามุมเท่า เนื่องจากการสะท้อนในวงกลมต้องทำมุมเท่าเดิมทุกครั้ง อันนี้คิดเองเออเองโดยไม่ได้พิสูจน์ แต่ผมทดลองจากการวาดรูปเหลี่ยมแนบในวงกลมอ่ะครับ จะชนขอบให้ได้ทุกมุม ต้องเป็นรูปเหลี่ยมด้านเท่ามุมเท่า
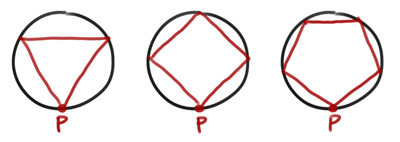
โจทย์ต้องการให้หาระยะทาง (ก็คือเส้นรอบรูป) และหามุมในการยิง ผมตั้งใจจะหามุมก่อนเพราะน่าจะง่ายกว่า คงอาศัยแค่บวกลบไล่มุมนิดหน่อย แล้วผมก็ลากรัศมีจากศูนย์กลางวงกลมไปยังจุดยอดมุมทุกจุด เกิดเป็นสามเหลี่ยมหน้าจั่ว 3 อัน, 4 อัน, 5 อัน ตามลำดับ ถ้าถามว่าทำไมถึงลากแบบนี้ ก็ยังไม่ได้คิดว่าจะไปต่อยังไงนะครับ แต่เป็นความรู้สึกว่าถ้าจะคิดทุกรูปให้ออกมาเป็นสูตรเดียวกัน ก็ควรจะหาลักษณะร่วมให้เจอ ซึ่งน่าจะเป็นบรรดาสามเหลี่ยมหน้าจั่วเหล่านี้แหละครับ แต่ถ้าลากแล้วไปต่อไม่ได้ ก็ค่อยเปลี่ยนวิธีใหม่ ไม่เป็นไรหนิ!
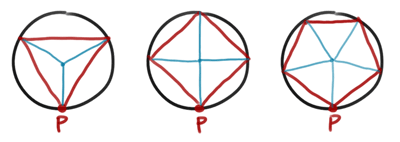
พอลากเสร็จแล้วเห็นทางไปเลยครับ เราหามุมยอดของสามเหลี่ยมหน้าจั่วโดยแบ่งมุมที่จุดศูนย์กลาง 360° ออกเท่าๆ กัน ได้เป็น 360°/n (นั่นคือ 120°, 90°, 72° ตามลำดับ) แล้วเราก็จะเขยิบไปหามุมที่ฐานได้ โดยเอามุมในสามเหลี่ยม 180° ลบด้วยมุมยอดนี้ แล้วหารสองแบ่งกัน นั่นคือ (180° - 360°/n)/2 = 90° - 180°/n
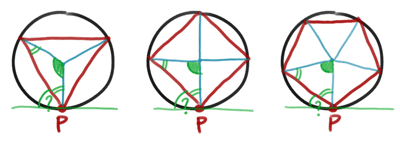
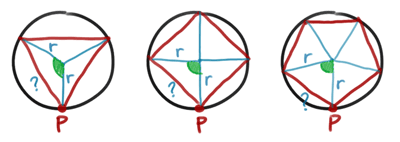
จากนั้นขั้นสุดท้ายหามุมในการยิง ซึ่งเราเห็นอยู่ว่าแขนของมุม คือรัศมีที่ลากขึ้นนี้ "ตั้งฉาก" กับเส้นสัมผัสวงกลมเสมอ ดังนั้นมุมที่ฐานกับมุมในการยิงต้องบวกกันได้มุมฉาก ก็สรุปว่า มุมในการยิงเท่ากับ 90° - มุมที่ฐาน = 90° - (90° - 180°/n) = 180°/n นั่นเอง
สรุปได้มุมในการยิงแล้วครับ คือ 180°/n เช่นสามเหลี่ยมก็ยิง 60°, สี่เหลี่ยมยิง 45°, ห้าเหลี่ยมยิง 36°, ร้อยเหลี่ยมยิง 1.8° ฯลฯ และจะเห็นว่าสูตรนี้ใช้กับการยิงสะท้อน 90° ได้ด้วย คือแทนค่า n=2 นั่นเอง เจ๋งจริงๆ (เรียกว่ารูป 2 เหลี่ยมคงได้มั้ง ฮ่าๆ)
ถ้าสังเกตจะเห็นว่ามาถึงตอนนี้เราเพิ่งใช้ความรู้ระดับ ม.ต้น เท่านั้นเอง หรืออาจจะมีวิธีที่สั้นกว่านี้ด้วย แต่คิดแบบไหนได้ก็ทำแบบนั้นก่อนดีแล้วครับ ถ้ามันไม่ได้ยาวยืดจนเกินไปนะ ^ ^
ส่วนการหาระยะทางรวม หรือเส้นรอบรูป n เหลี่ยม ในเมื่อได้ลากสามเหลี่ยมหน้าจั่วเอาไว้แล้ว ก็จะเห็นเลยว่าใช้ขนาดมุมยอด (360°/n) กับแขนของสามเหลี่ยม (ซึ่งก็คือรัศมี r) ก็จะหาความยาวฐานได้ทันที โดยอาศัยอัตราส่วน sin แบบง่ายๆ หรืออยากเล่นท่ายากก็ใช้กฎของโคไซน์ (cos) ก็ได้ครับ ตรงนี้เป็นความรู้ ม.5 ละ แต่ก็เป็นการหยิบมาแค่สูตรเดียวสั้นๆ ก็จบข้อได้เลย
วิธีที่ 1. การคิดด้วยอัตราส่วน sin เราแค่ลากส่วนสูงของสามเหลี่ยม ซึ่งจะแบ่งครึ่งมุมยอดและความยาวฐานพอดี เกิดสามเหลี่ยมมุมฉาก 2 รูป เราก็เขียน sin ได้เลยแบบวิชาคณิตพื้นฐาน (หรือที่ชอบพูดกันในวิชาฟิสิกส์ว่า "แตกแรง") ก็จะได้ด้านฐานยาว r sin(180°/n) คูณ 2
ดังนั้น ระยะทางรวม n ด้าน (ทุกด้านยาวเท่ากัน) = n 2r sin(180°/n)
หรือ n d sin(180°/n) เมื่อ d คือเส้นผ่านศูนย์กลางนั่นเองครับ
วิธีที่ 2. สมมติจะคิดด้วยกฎของ cos จะได้ความยาวด้าน = √r² + r² - 2(r)(r)cos(360°/n)
ดึง r² ที่เป็นตัวร่วมออกแล้วถอดรู้ทได้ ก็จะเป็น = √2 - 2cos(360°/n) ∙ r
ดังนั้น ระยะทางรวม n ด้าน = n ∙ √2 - 2cos(360°/n) ∙ r
จากนั้นเราสามารถจัดรูป cos ให้สั้นลงได้โดยอาศัยสูตร (1-cos2A)/2 = sin²A
ซึ่งก็จะถอดรู้ทได้ และออกมาเท่ากับวิธีแรกพอดีเปี๊ยบ (ตรงนี้ลองทดเองนะครับ)
ลองแทนค่าดูเพื่อความมั่นใจ เช่น แบบสั้นที่สุด n=2 (มุมยิง 90°) จะได้ระยะทางรวม 2(2)r = 4r
สามเหลี่ยม n=3 (มุมยิง 60°) จะได้ระยะทางรวม 3(√3)r ..ฯลฯ
ทดลอง n=100 (มุม 1.8°) กดเครื่องคิดเลขได้ระยะทางประมาณ 6.28r เกือบเท่า 2πr ก็แสดงว่าคิดถูกแล้วล่ะคร้าบ
สรุปแล้ว บทความนี้ก็เป็นการแสดงตัวอย่างหนึ่งให้ดูครับว่าบางครั้งโจทย์ที่ดูเหมือนยาก เพราะเราไม่เคยรู้เรื่องในวงการนั้นมาก่อน เช่นโมเดลเกี่ยวกับเสียงดนตรี เรายังคงสามารถแปลงมาอยู่ในรูปโจทย์คณิตศาสตร์ที่เราเจอประจำได้ และนอกจากนั้นเมื่อได้ลองลงมือทดแล้ว อาจพบว่าอาศัยหลักการคิดที่ง่ายกว่าโจทย์เอ็นท์มากๆ อีกต่างหากครับ
สงสัยกรณีรูปดาวแฉกๆ ค่อยมาดูกันต่อในตอนหน้าดีกว่า ขอบอกล่วงหน้าว่าคิดวิธีเดียวกันน่ะแหละครับ แต่ที่อาจจะยากหน่อยคือการสรุปกรณีทั้งหมดของดาว ว่ามีกี่แบบ.. ยังไงลองไปนึกกันเล่นๆ ก่อนนะครับ แล้วมาว่ากันต่อพรุ่งนี้เด้อ ^ ^
จากที่ได้เกริ่นไปแล้วว่าผมไม่ได้เป็นคนที่ชอบคิดเลขเป็นชีวิตจิตใจ แถมยังพยายามไม่คิดถ้าไม่จำเป็นอีกต่างหาก (แต่เรื่องที่ผมมองว่าจำเป็นอาจจะมีเยอะก็ได้นะครับ อิๆ) ดังนั้นนอกจากเวลาที่สอนพิเศษและเวลาทำหนังสือแล้ว โอกาสจะได้ใช้ความรู้ระดับ ม.ปลาย ในชีวิตจริงนั้นมีน้อยเหลือเกิน ที่ทำบ่อยก็แค่บวกลบคูณหารแบบประถมเวลาจะซื้อของ เหมือนกับทุกคนนั่นแหละครับ
เมื่อหลายวันก่อน เพื่อนผมอีกคนหนึ่งที่ทำงานเป็นโปรดิวเซอร์อัลบั้มเพลง (และเป็นคนที่มีความคิดและมุมมองก้าวล้ำไปไกลกว่าเพื่อนร่วมรุ่นมาตลอด) ได้ส่งโจทย์ข้อหนึ่งมาให้ผมใช้ความรู้ทางคณิตศาสตร์ช่วยแก้ให้ ที่จริงมันเป็นโมเดลเกี่ยวกับการเดินทางสะท้อนของเสียงภายในหน้าตัดวงกลม ซึ่งเขาบอกว่าเกิดนิมิตขึ้นขณะเคลิ้มๆ กึ่งหลับกึ่งตื่นครับ
ผมดูโจทย์ข้อนี้ในมุมคณิตศาสตร์แล้ว มีทั้งแง่มุมน่ารัก ท้าทาย และไม่ยากเกิน ม.ปลาย (ถ้ายากผมก็ไม่คิดหรอกครับ ฮ่าๆๆ) ประจวบกับไม่ได้สอนพิเศษมาหลายเดือน จนบางเวลาสมองซีกซ้ายมันตื้อๆ ไม่ค่อยแล่น เลยตื่นเต้นรีบหยิบกระดาษขึ้นมาทดในทันที พอแก้จนเสร็จก็รู้สึกว่าได้ไอเดียใหม่ๆ จากงานนี้หลายอย่าง คิดว่าเอามาเขียนบทความดีกว่า อย่างน้อยที่สุดน้องๆ นักเรียนก็คงได้เห็นว่าเวลาเจอโจทย์แล้วจะค่อยๆ คิดจนจบได้ยังไง.. นะครับ ^ ^
| คือเวลาสอนพิเศษเนี่ย ถ้าเจอโจทย์ที่น้องเอามาถามแล้วผมคิดไม่ออกในทันที ผมไม่เคยรู้สึกอายหรือเสียหน้าเลยครับ แต่จะขอเวลานั่งคิดเดี๋ยวนั้นเลย ให้น้องๆ ได้เห็นว่าเวลาเจอโจทย์ที่คิดไม่ออก ผมจะไล่ลำดับความรู้ยังไง ตั้งแต่เริ่มหาวิธีการตะล่อมๆ จนกระทั่งจบลุล่วงข้อนั้นไปได้ ซึ่งบางครั้งก็ไม่ได้ใช้วิธีที่ดีที่สุด บางครั้งก็เหมือนเส้นผมบังภูเขา หรือบางครั้งคิดนานเกินไปแล้วยังไม่ออก ผมก็จะขอเอากลับไปคิดต่อที่บ้านแล้วคราวหน้าจะมาตอบ (แล้วก็ต่างฝ่ายต่างลืมทุกที ถือเป็นทางเอาตัวรอดทางหนึ่งครับ 555) ผมมองว่าเรื่องการคิดสดให้ดูนี้ เป็นประสบการณ์อันจำเป็นอย่างหนึ่ง ที่ผู้เรียนสมควรได้รู้ได้เห็น แต่ไม่ค่อยได้เจอจากคุณครูที่ไหนเลยนะครับ ก็อยากฝากไอเดียนี้ไปยังคุณครูและติวเตอร์ด้วยครับ |
เอาล่ะ มาดูโจทย์ที่ว่ากันดีกว่าครับ
=============================================
กำหนดวงกลม C มีรัศมี r และมีจุด P เป็นจุดหนึ่งบนเส้นรอบวง จากจุดนี้สามารถยิง (ลาก) เส้นตรงออกไปสะท้อนที่ผิววงกลมได้ แนวการเดินที่สนใจคือแนวที่สะท้อนจนกลับมาถึงจุด P เท่านั้น โดยจะสะท้อนกี่ครั้งก็ได้ (คุณผู้อ่านลองวาดรูปตามไปด้วยแล้วจะเห็นความสนุกครับ)
เช่น แนวเดินที่สั้นที่สุดคือการยิงผ่านจุดศูนย์กลาง จะสะท้อนขอบวงกลมฝั่งตรงข้ามแล้วย้อนกลับมาที่จุด P ในทันที สรุประยะทางได้เท่ากับ 4r และมุมที่ยิงออกไปเท่ากับ 90° (เทียบกับเส้นสัมผัส ณ จุด P)
เข้าสู่คำถามนะครับ
1. ถ้าสมมติยิงทำมุม 60° จะเกิดการสะท้อนสองครั้งแล้วกลับมาที่จุดเดิม เป็นรูปสามเหลี่ยมด้านเท่าพอดี หรือถ้ายิงทำมุม 45° จะเกิดรูปสี่เหลี่ยมจัตุรัส ฯลฯ เหล่านี้เรียกว่ากรณี "n เหลี่ยมด้านเท่า"
อยากให้หาสูตรคำนวณระยะทางการวิ่งจนครบรอบ เมื่อกำหนดค่า n ต่างๆ (ก็แสดงว่าถ้า n มีค่ามากขึ้นเรื่อยๆ คำตอบจะต้องเข้าใกล้เส้นรอบวง 2πr) และบอกด้วยว่ามุมที่ยิงในแต่ละรูปต้องมีค่าเท่าไร
2. ถ้ายิงทำมุม (คาดว่า) 72° จะเกิดการสะท้อนเป็นรูปดาวห้าแฉกแล้วจึงกลับจุดเดิมพอดี แบบนี้ถือเป็นกรณีที่เส้นทางเดินตัดกันเป็น "รูปดาวแฉกๆ"
คำถามคือ จะสรุปการเดินทางเป็นลักษณะต่างๆ ได้อย่างไรบ้าง และให้หาสูตรคำนวณระยะทาง กับมุมที่ยิงด้วยเหมือนข้อแรก
=============================================
วาดเสร็จแล้วดูเหมือนเป็นคำถามที่ยากนะครับ กรณีรูป n เหลี่ยมนี่ยังไม่เท่าไร ยังพอจะได้เห็นในข้อสอบกันบ้าง แต่กรณีดาวแฉกๆ มันเกินสิ่งที่เราคุ้นเคยไปแล้ว จินตนาการไปถึงยากจัง แล้วดาวมันก็มีได้ไม่รู้กี่ร้อยกี่พันแบบ.. แต่เมื่อผมคิดจนเสร็จ ก็พบว่ามันใช้ความรู้เสี้ยวเดียวของตรีโกณ (ม.5) เท่านั้นเองครับ! คือสามารถเอาไปออกข้อสอบเอ็นท์ได้เลย และเป็นข้อสอบประเภทที่ "ดูยาก แต่เฉลยกลับไม่ค่อยมีอะไร" อีกต่างหาก
ถ้าใครอยากทดสอบความรู้ที่มี โดยเฉพาะข้อ 1. ซึ่งควรจะคิดได้ทุกคน ก็ลองหยิบกระดาษปากกามาลุยก่อนเลยครับ การคิดได้เองไม่เหมือนรอฟังเฉลยนะครับ (ใครที่เรียนถึง ม.5 แล้ว แต่คิดข้อ 1. ไม่ได้ ควรพิจารณาตนเองด่วน!) ..ส่วนข้อ 2. ยากหน่อย แต่ถ้าใครคิดคำตอบได้ ก็จะเกิดพุทธิไอเดียเท่ากับที่ผมได้มาแล้วจากโจทย์นี้เช่นกันครับ ถือว่าคุ้มอย่างยิ่ง ^ ^
... หลังจากลองวาดรูปหรือทดเองแล้ว ก็มาดูขั้นตอนที่ผมคิดกันบ้างนะครับ ...
เริ่มจากข้อแรก ผมลองวาดวงกลมแล้วใส่ 3 เหลี่ยม, 4 เหลี่ยม, 5 เหลี่ยม ลงไปอย่างละรูป แล้วก็พบข้อมูลเบื้องต้นว่า ต้องเป็นแบบด้านเท่ามุมเท่า เนื่องจากการสะท้อนในวงกลมต้องทำมุมเท่าเดิมทุกครั้ง อันนี้คิดเองเออเองโดยไม่ได้พิสูจน์ แต่ผมทดลองจากการวาดรูปเหลี่ยมแนบในวงกลมอ่ะครับ จะชนขอบให้ได้ทุกมุม ต้องเป็นรูปเหลี่ยมด้านเท่ามุมเท่า

โจทย์ต้องการให้หาระยะทาง (ก็คือเส้นรอบรูป) และหามุมในการยิง ผมตั้งใจจะหามุมก่อนเพราะน่าจะง่ายกว่า คงอาศัยแค่บวกลบไล่มุมนิดหน่อย แล้วผมก็ลากรัศมีจากศูนย์กลางวงกลมไปยังจุดยอดมุมทุกจุด เกิดเป็นสามเหลี่ยมหน้าจั่ว 3 อัน, 4 อัน, 5 อัน ตามลำดับ ถ้าถามว่าทำไมถึงลากแบบนี้ ก็ยังไม่ได้คิดว่าจะไปต่อยังไงนะครับ แต่เป็นความรู้สึกว่าถ้าจะคิดทุกรูปให้ออกมาเป็นสูตรเดียวกัน ก็ควรจะหาลักษณะร่วมให้เจอ ซึ่งน่าจะเป็นบรรดาสามเหลี่ยมหน้าจั่วเหล่านี้แหละครับ แต่ถ้าลากแล้วไปต่อไม่ได้ ก็ค่อยเปลี่ยนวิธีใหม่ ไม่เป็นไรหนิ!

| ตรงนี้ล่ะครับ จุดต่างของคนที่ทำคะแนนได้ดีกับไม่ดี ก็คือเรื่องการกล้าทดลองนี่เอง ระหว่างสอนจะเห็นเลยครับ น้องสองคนมีความรู้เท่ากันแต่พอสั่งให้ทำโจทย์ปุ๊บ คนนึงลงมือขีดๆ เขียนๆ ถูกไม่ถูกไม่รู้ล่ะแต่ลุยล่วงหน้าไปแล้ว ไปหาทางออกเอาทีหลัง แต่อีกคนกลับนั่งนิ่งไม่ไหวติง ผ่านไปสิบวินาทีก็เงยหน้าขึ้นมาพูดว่า "ทำยังไงอ่ะพี่นวย!" (นี่ถ้าเป็นการทำแบบฝึกหัด อ่านโจทย์เสร็จไม่เกินสิบวิ.คงแอบเปิดเฉลย เพราะไม่รู้จะถามใคร) ก็คงจะเดาได้ว่าคะแนนสอบออกมา คนแรกได้ผลดีกว่าแน่นอนครับ |
พอลากเสร็จแล้วเห็นทางไปเลยครับ เราหามุมยอดของสามเหลี่ยมหน้าจั่วโดยแบ่งมุมที่จุดศูนย์กลาง 360° ออกเท่าๆ กัน ได้เป็น 360°/n (นั่นคือ 120°, 90°, 72° ตามลำดับ) แล้วเราก็จะเขยิบไปหามุมที่ฐานได้ โดยเอามุมในสามเหลี่ยม 180° ลบด้วยมุมยอดนี้ แล้วหารสองแบ่งกัน นั่นคือ (180° - 360°/n)/2 = 90° - 180°/n

จากนั้นขั้นสุดท้ายหามุมในการยิง ซึ่งเราเห็นอยู่ว่าแขนของมุม คือรัศมีที่ลากขึ้นนี้ "ตั้งฉาก" กับเส้นสัมผัสวงกลมเสมอ ดังนั้นมุมที่ฐานกับมุมในการยิงต้องบวกกันได้มุมฉาก ก็สรุปว่า มุมในการยิงเท่ากับ 90° - มุมที่ฐาน = 90° - (90° - 180°/n) = 180°/n นั่นเอง
| ในตอนทำจริง ผมไม่ได้ค่อยๆ คิดเลขไปทีละขั้นตอนแบบนี้นะครับ เพราะถ้าไม่ใช่โจทย์หินจริงๆ เนี่ย จะต้องเห็นทางไปล่วงหน้า 2-3 ขั้นตอนก่อน แล้วจึงจะลงมือคิดเลข ..อย่างในข้อนี้ พอผมลากสามเหลี่ยมหน้าจั่วเสร็จแล้ว ความคิดก็ปรู๊ดเข้ามา เออแบบนี้เราหามุมยอดได้นะ (แต่จะต้องหาหรือเปล่ายังไม่รู้ เดี๋ยวค่อยว่ากัน) งั้นถ้ารู้มุมยอดก็จะรู้มุมที่ฐานได้ด้วยอ่ะสิ เฮ้ยพอรู้มุมที่ฐานก็รู้มุมในการยิงที่เขาถามด้วย อ้าวจบเลยสิ! คิดได้ดังนี้แล้วก็เริ่มลงมือทดครับ คนที่อ่านเฉลยในหนังสือลูกเดียว ไม่ฝึกเองเลย จะไปติดขัดที่จุดนี้ครับ อ่านแล้วรู้ขั้นตอนการคิดจนจบก็จริง แต่คิดเองไม่ได้เลย เพราะคนเขียนเฉลยเขาไม่ได้บอกว่ามองยังไงก่อนลงมือทำ.. ดังนั้นการใช้งานเฉลยให้ถูกวิธี เราควรเริ่มคิดไปได้สักหน่อยนึงก่อนครับ ไปติดขัดกลางทางแล้วค่อยดูเฉลยเพื่อให้เห็นทางไป |
สรุปได้มุมในการยิงแล้วครับ คือ 180°/n เช่นสามเหลี่ยมก็ยิง 60°, สี่เหลี่ยมยิง 45°, ห้าเหลี่ยมยิง 36°, ร้อยเหลี่ยมยิง 1.8° ฯลฯ และจะเห็นว่าสูตรนี้ใช้กับการยิงสะท้อน 90° ได้ด้วย คือแทนค่า n=2 นั่นเอง เจ๋งจริงๆ (เรียกว่ารูป 2 เหลี่ยมคงได้มั้ง ฮ่าๆ)
การลองแทนค่า n=100 รูปร้อยเหลี่ยมเนี่ย ก็เป็นอีกสิ่งหนึ่งที่บางคนมองว่าจะตลกไปไหน แต่บางคนก็จะเข้าใจว่ามีความหมายครับ เราแทนค่าที่มันสุดกู่ขนาดนี้ก็เพื่อตรวจสอบว่าคำตอบที่เราคิดมาเนี่ยจะถูกจริงหรือเปล่านั่นเอง อย่าง 1.8° ลองวาดรูปก็ไม่ได้ดูขัดแย้งอะไร จึงน่าจะถูกแล้วล่ะครับ |
ถ้าสังเกตจะเห็นว่ามาถึงตอนนี้เราเพิ่งใช้ความรู้ระดับ ม.ต้น เท่านั้นเอง หรืออาจจะมีวิธีที่สั้นกว่านี้ด้วย แต่คิดแบบไหนได้ก็ทำแบบนั้นก่อนดีแล้วครับ ถ้ามันไม่ได้ยาวยืดจนเกินไปนะ ^ ^
ส่วนการหาระยะทางรวม หรือเส้นรอบรูป n เหลี่ยม ในเมื่อได้ลากสามเหลี่ยมหน้าจั่วเอาไว้แล้ว ก็จะเห็นเลยว่าใช้ขนาดมุมยอด (360°/n) กับแขนของสามเหลี่ยม (ซึ่งก็คือรัศมี r) ก็จะหาความยาวฐานได้ทันที โดยอาศัยอัตราส่วน sin แบบง่ายๆ หรืออยากเล่นท่ายากก็ใช้กฎของโคไซน์ (cos) ก็ได้ครับ ตรงนี้เป็นความรู้ ม.5 ละ แต่ก็เป็นการหยิบมาแค่สูตรเดียวสั้นๆ ก็จบข้อได้เลย

| ในขณะที่หลายคนมองออกว่าวิธีนี้ช่างเหมาะมากๆ แต่หลายคนก็มองไม่ออก โดยอาจจะเป็นแบบ (1) ไม่แม่นเรื่องตรีโกณ จำไม่ได้ว่ามีอะไรให้ใช้งานบ้าง หรือรู้จักแต่ใช้ไม่เป็น ถ้าไม่บอกก็ไม่รู้ว่าต้องใช้อะไร แบบนี้ต้องไปฝึกให้คุ้นเคยขึ้นนะครับ อย่าไปมองว่าเป็นการท่องสูตรทื่อๆ แต่ให้มองว่าแต่ละอันมันเอาไปใช้ได้เมื่อไรบ้าง (2) เรื่องตรีโกณพอจะได้ ถ้าข้อนี้เป็นตัวเลขล่ะทำเป็นเลยนะ แต่นี่สัญลักษณ์ตัวอักษร n, r อะไรก็ไม่รู้ย๊าวยาว "ข้ามดีกว่าว่ะข้อนี้" ทั้งที่ทำมาจวนจะจบข้ออยู่แล้วนี่แหละครับ อีกสองบรรทัดเอง แบบนี้น่าเสียดายนะ ต้องฝึกความใจสู้กว่านี้หน่อยครับ |
วิธีที่ 1. การคิดด้วยอัตราส่วน sin เราแค่ลากส่วนสูงของสามเหลี่ยม ซึ่งจะแบ่งครึ่งมุมยอดและความยาวฐานพอดี เกิดสามเหลี่ยมมุมฉาก 2 รูป เราก็เขียน sin ได้เลยแบบวิชาคณิตพื้นฐาน (หรือที่ชอบพูดกันในวิชาฟิสิกส์ว่า "แตกแรง") ก็จะได้ด้านฐานยาว r sin(180°/n) คูณ 2
ดังนั้น ระยะทางรวม n ด้าน (ทุกด้านยาวเท่ากัน) = n 2r sin(180°/n)
หรือ n d sin(180°/n) เมื่อ d คือเส้นผ่านศูนย์กลางนั่นเองครับ
วิธีที่ 2. สมมติจะคิดด้วยกฎของ cos จะได้ความยาวด้าน = √r² + r² - 2(r)(r)cos(360°/n)
ดึง r² ที่เป็นตัวร่วมออกแล้วถอดรู้ทได้ ก็จะเป็น = √2 - 2cos(360°/n) ∙ r
ดังนั้น ระยะทางรวม n ด้าน = n ∙ √2 - 2cos(360°/n) ∙ r
จากนั้นเราสามารถจัดรูป cos ให้สั้นลงได้โดยอาศัยสูตร (1-cos2A)/2 = sin²A
ซึ่งก็จะถอดรู้ทได้ และออกมาเท่ากับวิธีแรกพอดีเปี๊ยบ (ตรงนี้ลองทดเองนะครับ)
ลองแทนค่าดูเพื่อความมั่นใจ เช่น แบบสั้นที่สุด n=2 (มุมยิง 90°) จะได้ระยะทางรวม 2(2)r = 4r
สามเหลี่ยม n=3 (มุมยิง 60°) จะได้ระยะทางรวม 3(√3)r ..ฯลฯ
ทดลอง n=100 (มุม 1.8°) กดเครื่องคิดเลขได้ระยะทางประมาณ 6.28r เกือบเท่า 2πr ก็แสดงว่าคิดถูกแล้วล่ะคร้าบ
| เป็นยังไงกันบ้างครับ คิดกันได้เท่านี้หรือเปล่า ใครอ่านตามอย่างเดียวมาจนถึงบรรทัดนี้ โดยไม่ได้คิดเองเลย ขอบอกว่าคุณพลาดโอกาสการฝึกฝนไปข้อนึงซะแล้วครับ อย่างที่ผมบอกเสมอว่า คนที่เน้นอ่านเฉลยอย่างเดียว จะได้แต่พยักหน้าถูก ถูก ตามเขาไป แต่ให้ทำเองล่ะมือฝืดเขียนไม่ออกขึ้นมากะทันหันซะอย่างงั้น อิๆๆ |
สรุปแล้ว บทความนี้ก็เป็นการแสดงตัวอย่างหนึ่งให้ดูครับว่าบางครั้งโจทย์ที่ดูเหมือนยาก เพราะเราไม่เคยรู้เรื่องในวงการนั้นมาก่อน เช่นโมเดลเกี่ยวกับเสียงดนตรี เรายังคงสามารถแปลงมาอยู่ในรูปโจทย์คณิตศาสตร์ที่เราเจอประจำได้ และนอกจากนั้นเมื่อได้ลองลงมือทดแล้ว อาจพบว่าอาศัยหลักการคิดที่ง่ายกว่าโจทย์เอ็นท์มากๆ อีกต่างหากครับ
สงสัยกรณีรูปดาวแฉกๆ ค่อยมาดูกันต่อในตอนหน้าดีกว่า ขอบอกล่วงหน้าว่าคิดวิธีเดียวกันน่ะแหละครับ แต่ที่อาจจะยากหน่อยคือการสรุปกรณีทั้งหมดของดาว ว่ามีกี่แบบ.. ยังไงลองไปนึกกันเล่นๆ ก่อนนะครับ แล้วมาว่ากันต่อพรุ่งนี้เด้อ ^ ^
นวย 15/10/54 16:01
edit 31/3/2017 เพิ่มคำตอบความยาวในรูปของ sin ครับ
ตอนที่เขียนบทความนี้ มีแค่กฎของ cos อย่างเดียว (เพราะเป็นวิธีแรกที่คิดออก)
ซึ่งยากกว่าการใช้ sin เยอะมาก ทำไมมองข้ามไปซะได้ 555
ตอนที่เขียนบทความนี้ มีแค่กฎของ cos อย่างเดียว (เพราะเป็นวิธีแรกที่คิดออก)
ซึ่งยากกว่าการใช้ sin เยอะมาก ทำไมมองข้ามไปซะได้ 555
นวย 01/04/60 03:04 [ 1 ]