Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0439 จาก 0508
| กระทู้ที่ 0438 บทความ#2 : n เหลี่ยมแนบในวงกลม | ตั้งกระทู้ใหม่ | กระทู้ที่ 0440 บทความ#4 : (แค่)คุณคุ้นคูณ |
บทความ#3 : จะไปเป็นดาวโดดเด่น.. ได้ยังไง!ตอบ: 1, อ่าน: 9633
ตอนนี้ต่อเนื่องจากตอนที่แล้วนะครับ ต้องอ่านตอนที่แล้วก่อนจึงจะอ่านตอนนี้รู้เรื่อง หรือถ้าใครลืมโจทย์ไปแล้ว ก็ลองย้อนไปดูสักนิดก่อนนะครับ (เอ๊ะทำไมลืมไวจัง 555)
เมื่อวานที่เราคิดรูป n เหลี่ยมในคำถามแรกกัน ผมได้พยายามเขียนเน้นไปที่การคิดสดให้ดูทีละขั้นตอน เพื่อให้น้องๆ นักเรียนได้มีประสบการณ์ในด้านนี้ แต่มาถึงวันนี้ที่เราจะคิดรูปดาวแฉกๆ ในคำถามที่สอง ผมถือว่าเป็นส่วนของไอเดียเสริมแล้วล่ะครับ เป็นการเขียนเพื่อให้จบข้อโดยสมบูรณ์เท่านั้นเอง (หรือถ้าบอกว่าเขียนเพราะดีใจที่หาคำตอบได้ ก็จะใช่ที่สุดเลย ฮ่าๆ)
ดังนั้นถ้าใครอ่านไปแล้วงงงวย ก็อย่าเพิ่งเครียดไปครับ มันอาจจะยากเกินจริงๆ ก็ได้ เอาเป็นว่าตอนหน้าผมจะพยายามเขียนแค่เรื่องบวกลบคูณหารครับ ลดความปวดหัวลงหน่อยดีกว่า แหะๆ ^ ^"
- 1 -
รูปแบบที่เราจะมาสาละวนกันในวันนี้เรียกว่า "กรณีดาว n แฉก" ซึ่งจะเกิดเมื่อเส้นทางวิ่งนั้นตัดกันนะครับ จากการลองวาดรูปดาวในวงกลมขึ้นมาเล่นๆ หลายแบบไปเรื่อยๆ ห้าแฉก เจ็ดแฉก ฯลฯ ผมก็พบข้อสังเกตเบื้องต้นว่า "จุดที่เกิดการสะท้อนจะเรียงตัวกันเป็น n เหลี่ยมด้านเท่าเสมอเลย โดยจะเกิดดาวก็ต่อเมื่อเราเริ่มยิงไปที่จุดอื่นๆ แทนที่จะยิงไปจุดยอดที่ติดกันนั่นเอง"
เช่นรูป 5 เหลี่ยม ถ้าเริ่มยิงไปหาจุดยอดที่อยู่ติดกัน คือจุดที่ 1 หรือจุดที่ 4 มันจะเกิดเป็นห้าเหลี่ยมด้านเท่า ซึ่งคิดไปแล้วเมื่อวาน แต่ถ้าเริ่มยิงไปยังจุดที่ 2 หรือ 3 หรือเรียกง่ายๆ ว่ากระโดดทีละ 2 หรือ 3 จุด จะเกิดเป็นรูปดาว 5 แฉกขึ้นมาครับ (อ้อ! อย่าสะท้อนมั่วนะครับ ในผิววงกลมมุมตกกระทบกับมุมสะท้อนต้องเท่ากัน นั่นคือต้องกระโดดข้ามจุดทีละเท่ากันทุกครั้ง เพราะถ้าไม่เท่าได้ด้วย มันจะเกิดรูปดาวประหลาดๆ ได้อีกมหาศาลเลยล่ะ)
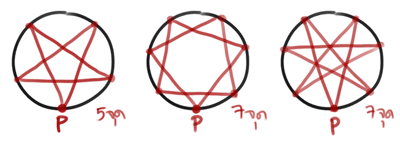
หรืออย่างรูปดาว 7 แฉก ก็ย่อมเกิดจากการยิงไปมาภายในรูป 7 เหลี่ยมครับ โดยถ้าเรายิงไปยังจุดที่ 2 ก็จะได้ผลแบบนึง ถ้ายิงไปยังจุดที่ 3 ก็ได้ผลอีกแบบนึง (ส่วนการยิงไปจุดที่ 4 และ 5 หรือเมื่อมุมยิงเกิน 90° เนี่ย เราจะไม่พูดถึงแล้วครับ เพราะจะเกิดผลเหมือนการยิงไปจุดที่ 2 และ 3 เพียงแต่วิ่งสวนกลับเท่านั้นเอง)
- 2 -
เอ้ากลับมาเรื่องดาวต่อครับ.. หลังจากได้ดาว 5 แฉกและ 7 แฉก ผมก็ลองพยายามวาดรูปดาวที่อยู่ใน 4 เหลี่ยม, 6 เหลี่ยม, 8 เหลี่ยมดูบ้างครับ จึงพบว่า "ระยะกระโดดที่เกิดดาวนั้น จะต้องหาร n ไม่ลงตัว" มิฉะนั้นรูปที่ได้จะกลายเป็นรูปเหลี่ยมที่เล็กลง และไม่เกิดดาว
เช่น รูปหกเหลี่ยม ถ้ากระโดดทีละ 2 จุด จะเกิดแค่สามเหลี่ยม (เพราะ 6/2 ลงตัว) หรือถ้ากระโดด 3 จุด จะเกิดการเด้งกลับมาที่เดิมทันที (เพราะ 6/3 ลงตัว) ส่วนรูปแปดเหลี่ยม จะต้องกระโดดทีละ 3 จุด จึงเกิดดาวได้ เพราะ 8/3 ไม่ลงตัว (แต่ห้ามกระโดดทีละ 2 หรือ 4 จุด เพราะหารลงตัว)
เรื่องนี้ผมลืมวาดรูปมาแปะ ลองวาดเองดูสิครับ สนุกดีนะ! ^ ^
มาถึงขณะนี้เราก็เลยยืนยันได้ว่า
- ดาว 4 แฉก ไม่มีในโลก (นอกโลกก็ไม่น่าจะมีนะครับ ฮ่าๆๆ)
- ดาว 5 แฉก มีได้แบบเดียว คือแบบ "5โดด2"
- ดาว 6 แฉก ก็สร้างไม่ได้ครับ ไม่มีในโลก
- ดาว 7 แฉก มีได้สองแบบ คือ "7โดด2" กับ "7โดด3"
- ดาว 8 แฉก มีได้แบบเดียว คือ "8โดด3"
- จำนวนแฉกมากกว่านี้ก็หาได้ด้วยหลักการเดียวกัน
ฉะนั้นนอกจากจำนวนเหลี่ยมคือ n แล้ว ในสูตรเราคงต้องเพิ่มตัวแปร k เข้ามาอีกสักตัวครับ ใช้แทนการกระโดดไปกี่จุด เช่นรูป 5 เหลี่ยมเกิดเมื่อ n=5 และ k=1, รูปดาว 5 แฉกเกิดเมื่อ n=5 และ k=2 (โดยค่า k ที่เราสนใจ จะไม่เกินครึ่งของ n ไม่งั้นจะเกิดรูปซ้ำที่วิ่งสวนกลับด้าน)
- 3 -
เท่านั้นไม่พอครับ มีใครสังเกตได้บ้างว่าในการลากรูปดาวนี้ แต่ละจุดจะลากผ่านเพียงครั้งเดียว ดังนั้น "แนวเดินทั้งหมดจะเป็นเส้นตรง n เส้นพอดี" (และยาวเท่ากันด้วยครับ เพราะระยะกระโดดคงที่) คือรูปดาว 5 แฉก จะเกิดจากเส้นตรง 5 เส้น หรือว่ารูปดาว 100 แฉก ก็จะต้องเกิดจากเส้นตรง 100 เส้น
ถามว่าทำไมถึงรู้ว่าจะไม่ใช้จุดซ้ำ ทำไมถึงรู้ว่าจะใช้ครบทุกจุด และทำไมถึงรู้ว่าจะกลับมาที่จุดเดิมพอดี ตรงนี้อาศัยความรู้ในเรื่องลำดับ (ม.5) ครับ ซึ่งอันที่จริงผมใช้วิธีลองยกตัวเลขแปลกๆ ขึ้นมาแล้วเขียนไล่เอาดื้อๆ เลย เช่น ดาวแบบ (11,4) จะได้แนวเดิน
P, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, P
(กลับมาถึงจุดเริ่มต้นก็คือจบ) จะเห็นว่าเดินทาง 11 ครั้งและไม่ซ้ำจุดกัน // ถ้าคุณผู้อ่านลองตั้งเลขขึ้นมาแล้วเขียนลำดับดู จะเห็นได้เองอย่างชัดเจนเลยครับ
เอาล่ะครับ พอเข้าใจลักษณะการเกิดของรูปดาวประมาณนึงแล้ว ก็มาคิดคำตอบเรื่องมุมการยิงและระยะทางกันดีกว่า ขั้นตอนตรงนี้สั้นมากครับเพราะเลียนแบบวิธีคิดของเมื่อวานได้ ซึ่งคุณผู้อ่านลองคิดเองก่อนก็ได้นะครับ แล้วค่อยมาเช็คว่าเราได้คำตอบตรงกันหรือเปล่า
ป.ล. ประเด็นที่น่าสนุกคือการสรุปรูปแบบของดาว ซึ่งก็เล่ามาจนหมดก๊อกซะแล้ว ผมเลยหมดกำลังใจจะเขียนต่อขึ้นมาทันทีครับ 555 แต่เพื่อให้บทความนี้จบลงโดยสวัสดิภาพ ก็ต้องเอาให้เสร็จล่ะเนาะ :P
=============================================
- 4 -
ในการหาคำตอบ ผมจะเริ่มจากหามุมก่อนเหมือนเดิมครับ เป็นการพยายามใช้สมองให้น้อยที่สุดอีกแล้ว ฮ่าๆ
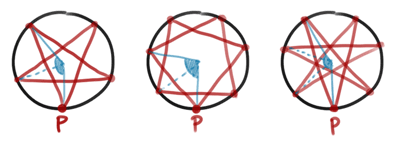
พอลากรัศมีให้เกิดสามเหลี่ยมหน้าจั่วขึ้นแล้ว จะเห็นได้ว่าขนาดของมุมยอด จากเดิม 360°/n คราวนี้มันใหญ่ขึ้นตามจำนวนจุดที่กระโดดครับ อย่างดาว 5 แฉก กระโดดทีละ 2 จุด มุมยอดก็เป็นสองเท่าของเดิม หรือดาว 7 แฉก แบบกระโดดทีละ 2 หรือ 3 จุด มุมยอดก็เป็น 2 หรือ 3 เท่าของเดิม
การที่กระโดดกี่จุด มุมก็เพิ่มไปเท่านั้น แบบนี้เราก็สรุปมุมยอดได้เป็น k ∙ 360°/n นั่นเองครับ เอา k ไปคูณมุมของเมื่อวานได้เลย (ขอเขียนเป็น 360°k/n ก็แล้วกัน) จากนั้นเมื่อเราไล่ไปหามุมที่ฐาน และมุมในการยิง ด้วยขั้นตอนเดิม ก็จะได้คำตอบมุมในการยิง = 180°k/n
คำตอบที่ได้ 180°k/n ผมมองว่าเป็นคำตอบที่สวยงามมากครับ เพราะถ้าเราเกิดแทนค่า k=1 หรือกระโดดทีละจุดเดียว ทั้งภาพและสูตรจะกลายเป็นกรณีเมื่อวานพอดี เมื่อเราคิดสูตรนี้เสร็จสูตรเดิมก็ไม่จำเป็นเลยครับ ใช้แทนกันได้เลย
แถมนี่ยังมีผลทำให้คำถามข้อ 1. กับข้อ 2. รวมร่างเป็นกรณีเดียวกันได้อย่างมหัศจรรย์ด้วย (เอ้า ใครจะไปคิดว่ารูป 7 เหลี่ยม กับรูปดาว 7 แฉก จะใช้สูตรเดียวกัน.. เนอะ) อย่างงี้พอจะเรียกว่าสวยงามได้หรือยังครับ อิๆๆ ^ ^
เท่านั้นไม่พอ การที่มีเศษส่วน k/n ปรากฏอยู่ ยังฟ้องด้วยว่า ถ้า k และ n ดันหารกันลงตัว คือทำให้ k กลายเป็น 1 ก็จะเกิดรูปเหลี่ยมด้านเท่าเหมือนเมื่อวานไปเลย (เช่น "6โดด2" จะได้เศษส่วนเป็น 2/6 = 1/3 เกิดรูปสามเหลี่ยมซะงั้น) นี่เป็นการยืนยันข้อสังเกตที่ว่ารูปดาวจะเกิดขึ้นได้ ต้องหารกันไม่ลงตัว
มันทำให้ผมฉุกคิดขึ้นได้ถึงกรณีที่ "หารกันไม่ลงตัว แต่ลดทอนได้บ้างอ่ะ" เช่น (10,4) หรือ (15,6) แบบนี้มันยังจะเกิดดาว 10 แฉกและ 15 แฉกหรือเปล่าหว่า? ..คงไม่ต้องวาดรูปหรือไล่ลำดับ เพราะดูจากสูตรท่าจะไม่เกิดซะแล้วครับ เพราะ 4/10 = 2/5 ก็แสดงว่าพอลากเสร็จจะเกิดผลลัพธ์เหมือนแบบ (5,2) เป๊ะ คือลากแค่ 5 ครั้งก็กลับมาจุดเริ่มต้นซะงั้น เช่นเดียวกับรูป (15,6) ก็จะได้ออกมาเป็นดาว (5,2) ด้วย
สุดท้ายเรามาคิดระยะทางหรือเส้นรอบรูป ก็หาด้านเดียวก่อนโดยอาศัยอัตราส่วน sin (หรือเล่นท่ายาก กฎของ cos) เช่นเดิม เพียงแต่เปลี่ยนมุมตรงกลางจาก 360°/n มาเป็น 360°k/n ส่วนจำนวนด้านทั้งหมดที่จะต้องคูณ ก็มี n ด้านเหมือนเดิมครับ
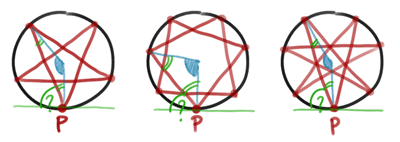
หลายคนคงจะนึกออกแล้วล่ะครับ ว่าคำตอบก็ก๊อปจากเมื่อวานมาได้เลย นั่นคือ n d sin(180°k/n) ครับ ตรงนี้มองในใจได้อีกแล้ว จะเห็นว่าสูตรที่ได้นี้ก็ครอบคลุมกรณีรูปเหลี่ยมด้านเท่า (k=1) ด้วยเช่นกัน.. อ้าว งั้นคำตอบทั้งหมดที่อุตส่าห์นั่งคิดเมื่อวานก็ไม่ได้เอาไปใช้เลยอ่ะสิ เวรกรรม! :P
หลังจากได้คำตอบครบถ้วนแล้ว ทีนี้ถ้าใครให้เราหาเส้นรอบรูป n เหลี่ยม หรือดาว n แฉก (ที่แนบในวงกลมได้) เราก็แค่หยิบไม้บรรทัดมาวัดเส้นผ่านศูนย์กลางวงกลม แล้วแทนค่าลงในสูตรนี้ตอบได้เลยครับ เจ๋งมั้ยล่ะ!! (แต่ถ้าเรามีไม้บรรทัดจริงๆ เอามาวัดความยาว 1 ด้านแล้วคูณด้วย n ซะเลย จะไม่ดีกว่าเหรอเนี่ย อิๆๆ)
เพื่อไม่ให้บทความตอนนี้ยืดเกินไป ผมก็จะขอตัดจบดื้อๆ ห้วนๆ แต่เพียงเท่านี้เลยครับ พบกันใหม่ตอนต่อไปในวันพรุ่งนี้ ซึ่งก็จะยังคงแนะหลักการเรียนเลขโดยอาศัยโจทย์เพียงข้อเดียวเหมือนเดิมคร้าบ (คราวนี้จะเอาตัวอย่างที่ง่ายสุดๆ แล้วล่ะ) ^ ^
เมื่อวานที่เราคิดรูป n เหลี่ยมในคำถามแรกกัน ผมได้พยายามเขียนเน้นไปที่การคิดสดให้ดูทีละขั้นตอน เพื่อให้น้องๆ นักเรียนได้มีประสบการณ์ในด้านนี้ แต่มาถึงวันนี้ที่เราจะคิดรูปดาวแฉกๆ ในคำถามที่สอง ผมถือว่าเป็นส่วนของไอเดียเสริมแล้วล่ะครับ เป็นการเขียนเพื่อให้จบข้อโดยสมบูรณ์เท่านั้นเอง (หรือถ้าบอกว่าเขียนเพราะดีใจที่หาคำตอบได้ ก็จะใช่ที่สุดเลย ฮ่าๆ)
ดังนั้นถ้าใครอ่านไปแล้วงงงวย ก็อย่าเพิ่งเครียดไปครับ มันอาจจะยากเกินจริงๆ ก็ได้ เอาเป็นว่าตอนหน้าผมจะพยายามเขียนแค่เรื่องบวกลบคูณหารครับ ลดความปวดหัวลงหน่อยดีกว่า แหะๆ ^ ^"
รูปแบบที่เราจะมาสาละวนกันในวันนี้เรียกว่า "กรณีดาว n แฉก" ซึ่งจะเกิดเมื่อเส้นทางวิ่งนั้นตัดกันนะครับ จากการลองวาดรูปดาวในวงกลมขึ้นมาเล่นๆ หลายแบบไปเรื่อยๆ ห้าแฉก เจ็ดแฉก ฯลฯ ผมก็พบข้อสังเกตเบื้องต้นว่า "จุดที่เกิดการสะท้อนจะเรียงตัวกันเป็น n เหลี่ยมด้านเท่าเสมอเลย โดยจะเกิดดาวก็ต่อเมื่อเราเริ่มยิงไปที่จุดอื่นๆ แทนที่จะยิงไปจุดยอดที่ติดกันนั่นเอง"
เช่นรูป 5 เหลี่ยม ถ้าเริ่มยิงไปหาจุดยอดที่อยู่ติดกัน คือจุดที่ 1 หรือจุดที่ 4 มันจะเกิดเป็นห้าเหลี่ยมด้านเท่า ซึ่งคิดไปแล้วเมื่อวาน แต่ถ้าเริ่มยิงไปยังจุดที่ 2 หรือ 3 หรือเรียกง่ายๆ ว่ากระโดดทีละ 2 หรือ 3 จุด จะเกิดเป็นรูปดาว 5 แฉกขึ้นมาครับ (อ้อ! อย่าสะท้อนมั่วนะครับ ในผิววงกลมมุมตกกระทบกับมุมสะท้อนต้องเท่ากัน นั่นคือต้องกระโดดข้ามจุดทีละเท่ากันทุกครั้ง เพราะถ้าไม่เท่าได้ด้วย มันจะเกิดรูปดาวประหลาดๆ ได้อีกมหาศาลเลยล่ะ)

หรืออย่างรูปดาว 7 แฉก ก็ย่อมเกิดจากการยิงไปมาภายในรูป 7 เหลี่ยมครับ โดยถ้าเรายิงไปยังจุดที่ 2 ก็จะได้ผลแบบนึง ถ้ายิงไปยังจุดที่ 3 ก็ได้ผลอีกแบบนึง (ส่วนการยิงไปจุดที่ 4 และ 5 หรือเมื่อมุมยิงเกิน 90° เนี่ย เราจะไม่พูดถึงแล้วครับ เพราะจะเกิดผลเหมือนการยิงไปจุดที่ 2 และ 3 เพียงแต่วิ่งสวนกลับเท่านั้นเอง)
| ในการทำข้อสอบ การรู้จักสรุปข้อสังเกตเบื้องต้นเป็นสิ่งสำคัญนะครับ เพราะมีข้อสอบจำนวนหนึ่งไม่ยอมบอกคุณลักษณะมาให้ครบถ้วน แต่จงใจไม่พูดบางเรื่อง ปล่อยให้เราฟันธงเพิ่มเองว่ามันต้องเป็นอย่างนั้นอย่างนี้ ซึ่งถ้าใครไม่ได้สรุปตามล่ะก็ จะเริ่มทำข้อนั้นไม่ได้ หรือทำไม่จบข้อเลยล่ะครับ (อย่างในโจทย์นี้ ถ้าผมไม่ได้สรุปดังข้อความในเครื่องหมายคำพูดข้างบนนู้น ก็คงไม่รู้จะคิดต่อไปยังไงเหมือนกัน) แต่ในทางกลับกัน! น้องๆ ต้องระวังอย่าไปสรุปเกินจริงนะครับ ตรงไหนไม่มั่นใจก็อย่าไปสรุปมัน ที่ผมเห็นบ่อยคือบางคนพอติดขัดทำต่อไม่ได้ เลยโมเมเอาตามที่เห็น ซึ่งโดยมากมันจะหลอกตา ..เฮ้ย นี่ไงสองเส้นนี้ยาวเท่ากัน! (ชัวร์เหรอ?) นี่ไงมุมนี้มันตั้งฉาก! (ชัวร์เหรอ?) ฯลฯ ไปทึกทักเองอย่างงั้นคำตอบมันก็ผิดสิครับ ยิ่งวาดรูปไม่ค่อยจะเป๊ะกันอยู่แล้วด้วยเนาะ :P |
เอ้ากลับมาเรื่องดาวต่อครับ.. หลังจากได้ดาว 5 แฉกและ 7 แฉก ผมก็ลองพยายามวาดรูปดาวที่อยู่ใน 4 เหลี่ยม, 6 เหลี่ยม, 8 เหลี่ยมดูบ้างครับ จึงพบว่า "ระยะกระโดดที่เกิดดาวนั้น จะต้องหาร n ไม่ลงตัว" มิฉะนั้นรูปที่ได้จะกลายเป็นรูปเหลี่ยมที่เล็กลง และไม่เกิดดาว
เช่น รูปหกเหลี่ยม ถ้ากระโดดทีละ 2 จุด จะเกิดแค่สามเหลี่ยม (เพราะ 6/2 ลงตัว) หรือถ้ากระโดด 3 จุด จะเกิดการเด้งกลับมาที่เดิมทันที (เพราะ 6/3 ลงตัว) ส่วนรูปแปดเหลี่ยม จะต้องกระโดดทีละ 3 จุด จึงเกิดดาวได้ เพราะ 8/3 ไม่ลงตัว (แต่ห้ามกระโดดทีละ 2 หรือ 4 จุด เพราะหารลงตัว)
เรื่องนี้ผมลืมวาดรูปมาแปะ ลองวาดเองดูสิครับ สนุกดีนะ! ^ ^
มาถึงขณะนี้เราก็เลยยืนยันได้ว่า
- ดาว 4 แฉก ไม่มีในโลก (นอกโลกก็ไม่น่าจะมีนะครับ ฮ่าๆๆ)
- ดาว 5 แฉก มีได้แบบเดียว คือแบบ "5โดด2"
- ดาว 6 แฉก ก็สร้างไม่ได้ครับ ไม่มีในโลก
- ดาว 7 แฉก มีได้สองแบบ คือ "7โดด2" กับ "7โดด3"
- ดาว 8 แฉก มีได้แบบเดียว คือ "8โดด3"
- จำนวนแฉกมากกว่านี้ก็หาได้ด้วยหลักการเดียวกัน
ฉะนั้นนอกจากจำนวนเหลี่ยมคือ n แล้ว ในสูตรเราคงต้องเพิ่มตัวแปร k เข้ามาอีกสักตัวครับ ใช้แทนการกระโดดไปกี่จุด เช่นรูป 5 เหลี่ยมเกิดเมื่อ n=5 และ k=1, รูปดาว 5 แฉกเกิดเมื่อ n=5 และ k=2 (โดยค่า k ที่เราสนใจ จะไม่เกินครึ่งของ n ไม่งั้นจะเกิดรูปซ้ำที่วิ่งสวนกลับด้าน)
เท่านั้นไม่พอครับ มีใครสังเกตได้บ้างว่าในการลากรูปดาวนี้ แต่ละจุดจะลากผ่านเพียงครั้งเดียว ดังนั้น "แนวเดินทั้งหมดจะเป็นเส้นตรง n เส้นพอดี" (และยาวเท่ากันด้วยครับ เพราะระยะกระโดดคงที่) คือรูปดาว 5 แฉก จะเกิดจากเส้นตรง 5 เส้น หรือว่ารูปดาว 100 แฉก ก็จะต้องเกิดจากเส้นตรง 100 เส้น
ถามว่าทำไมถึงรู้ว่าจะไม่ใช้จุดซ้ำ ทำไมถึงรู้ว่าจะใช้ครบทุกจุด และทำไมถึงรู้ว่าจะกลับมาที่จุดเดิมพอดี ตรงนี้อาศัยความรู้ในเรื่องลำดับ (ม.5) ครับ ซึ่งอันที่จริงผมใช้วิธีลองยกตัวเลขแปลกๆ ขึ้นมาแล้วเขียนไล่เอาดื้อๆ เลย เช่น ดาวแบบ (11,4) จะได้แนวเดิน
P, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, P
(กลับมาถึงจุดเริ่มต้นก็คือจบ) จะเห็นว่าเดินทาง 11 ครั้งและไม่ซ้ำจุดกัน // ถ้าคุณผู้อ่านลองตั้งเลขขึ้นมาแล้วเขียนลำดับดู จะเห็นได้เองอย่างชัดเจนเลยครับ
| บางคนอาจจะคิดในใจว่าแหม แค่วาดรูปดาวขึ้นมา 3-4 อัน ก็รู้แล้วว่าดาวเกิดจากการลากข้ามจุด ไม่เห็นจะต้องคิดเยอะขนาดที่เล่ามาตั้งแต่ต้นเลย.. ก็ต้องขอย้ำครับว่าโจทย์ที่ได้รับมอบหมาย เขาอยากให้เราหาว่าการสะท้อนเป็นไปได้ในลักษณะไหนบ้างด้วย ถ้าเราตอบไปแค่เท่าที่วาดขึ้นมา อาจจะเป็นคำตอบที่ไม่ครบถ้วนทุกกรณีก็ได้นะครับ ^ ^ |
เอาล่ะครับ พอเข้าใจลักษณะการเกิดของรูปดาวประมาณนึงแล้ว ก็มาคิดคำตอบเรื่องมุมการยิงและระยะทางกันดีกว่า ขั้นตอนตรงนี้สั้นมากครับเพราะเลียนแบบวิธีคิดของเมื่อวานได้ ซึ่งคุณผู้อ่านลองคิดเองก่อนก็ได้นะครับ แล้วค่อยมาเช็คว่าเราได้คำตอบตรงกันหรือเปล่า
ป.ล. ประเด็นที่น่าสนุกคือการสรุปรูปแบบของดาว ซึ่งก็เล่ามาจนหมดก๊อกซะแล้ว ผมเลยหมดกำลังใจจะเขียนต่อขึ้นมาทันทีครับ 555 แต่เพื่อให้บทความนี้จบลงโดยสวัสดิภาพ ก็ต้องเอาให้เสร็จล่ะเนาะ :P
=============================================
ในการหาคำตอบ ผมจะเริ่มจากหามุมก่อนเหมือนเดิมครับ เป็นการพยายามใช้สมองให้น้อยที่สุดอีกแล้ว ฮ่าๆ

พอลากรัศมีให้เกิดสามเหลี่ยมหน้าจั่วขึ้นแล้ว จะเห็นได้ว่าขนาดของมุมยอด จากเดิม 360°/n คราวนี้มันใหญ่ขึ้นตามจำนวนจุดที่กระโดดครับ อย่างดาว 5 แฉก กระโดดทีละ 2 จุด มุมยอดก็เป็นสองเท่าของเดิม หรือดาว 7 แฉก แบบกระโดดทีละ 2 หรือ 3 จุด มุมยอดก็เป็น 2 หรือ 3 เท่าของเดิม
การที่กระโดดกี่จุด มุมก็เพิ่มไปเท่านั้น แบบนี้เราก็สรุปมุมยอดได้เป็น k ∙ 360°/n นั่นเองครับ เอา k ไปคูณมุมของเมื่อวานได้เลย (ขอเขียนเป็น 360°k/n ก็แล้วกัน) จากนั้นเมื่อเราไล่ไปหามุมที่ฐาน และมุมในการยิง ด้วยขั้นตอนเดิม ก็จะได้คำตอบมุมในการยิง = 180°k/n
| ขอสารภาพว่าผมไม่ได้ทดใหม่หรอกครับ เพราะเราสามารถอุปนัยหรือ "มองในใจ" ได้เลยว่ามันต้องตอบรูปนี้ การมองในใจจะช่วยประหยัดเวลาทำข้อสอบได้มากเลยครับ ใครที่ไม่คล่องลองไปฝึกกันดูนะครับ แต่ต้องมองอย่างมีหลักการนะ ไม่ใช่จับแพะชนแกะ เห็นอะไรคล้ายหน่อยแล้วจับมาตอบเลยนะครับ อันนั้นคือมั่ว! |
คำตอบที่ได้ 180°k/n ผมมองว่าเป็นคำตอบที่สวยงามมากครับ เพราะถ้าเราเกิดแทนค่า k=1 หรือกระโดดทีละจุดเดียว ทั้งภาพและสูตรจะกลายเป็นกรณีเมื่อวานพอดี เมื่อเราคิดสูตรนี้เสร็จสูตรเดิมก็ไม่จำเป็นเลยครับ ใช้แทนกันได้เลย
แถมนี่ยังมีผลทำให้คำถามข้อ 1. กับข้อ 2. รวมร่างเป็นกรณีเดียวกันได้อย่างมหัศจรรย์ด้วย (เอ้า ใครจะไปคิดว่ารูป 7 เหลี่ยม กับรูปดาว 7 แฉก จะใช้สูตรเดียวกัน.. เนอะ) อย่างงี้พอจะเรียกว่าสวยงามได้หรือยังครับ อิๆๆ ^ ^
เท่านั้นไม่พอ การที่มีเศษส่วน k/n ปรากฏอยู่ ยังฟ้องด้วยว่า ถ้า k และ n ดันหารกันลงตัว คือทำให้ k กลายเป็น 1 ก็จะเกิดรูปเหลี่ยมด้านเท่าเหมือนเมื่อวานไปเลย (เช่น "6โดด2" จะได้เศษส่วนเป็น 2/6 = 1/3 เกิดรูปสามเหลี่ยมซะงั้น) นี่เป็นการยืนยันข้อสังเกตที่ว่ารูปดาวจะเกิดขึ้นได้ ต้องหารกันไม่ลงตัว
มันทำให้ผมฉุกคิดขึ้นได้ถึงกรณีที่ "หารกันไม่ลงตัว แต่ลดทอนได้บ้างอ่ะ" เช่น (10,4) หรือ (15,6) แบบนี้มันยังจะเกิดดาว 10 แฉกและ 15 แฉกหรือเปล่าหว่า? ..คงไม่ต้องวาดรูปหรือไล่ลำดับ เพราะดูจากสูตรท่าจะไม่เกิดซะแล้วครับ เพราะ 4/10 = 2/5 ก็แสดงว่าพอลากเสร็จจะเกิดผลลัพธ์เหมือนแบบ (5,2) เป๊ะ คือลากแค่ 5 ครั้งก็กลับมาจุดเริ่มต้นซะงั้น เช่นเดียวกับรูป (15,6) ก็จะได้ออกมาเป็นดาว (5,2) ด้วย
| เราเอาหลักการนี้ไปนับจำนวนดาวที่มีแฉกต่างๆ กันได้เลยนะครับเนี่ย เช่น ดาว 100 แฉกมีทั้งหมดกี่แบบ? ก็นับไปตั้งแต่ (100,3), (100,7), (100,11), ... จนถึง (100,49) เอาเฉพาะตัวเลขที่ตัดกันไม่ได้นั่นเองครับ (หรือถ้าพูดให้ดูยากๆ หน่อย ต้องบอกว่าหาจำนวนที่ "เป็นจำนวนเฉพาะสัมพัทธ์กับ 100" นั่นเอง) รวมกี่แบบก็ไม่รู้เพราะผมก็ยังไม่ได้นับ ฮ่าๆๆ แต่ถ้าใครขยันอยากนับ ขอแนะนำให้หาจำนวนที่ตัดเลขได้ (หรือมีตัวประกอบร่วมกับ 100) แล้วมาหักออกดีกว่านะครับ ประหยัดสมองกว่า.. คุณครูลองนำไปออกข้อสอบในเรื่องจำนวนจริง (ม.4) หรือหลักการนับ (ม.6) ดูไหมครับ อิๆๆ |
สุดท้ายเรามาคิดระยะทางหรือเส้นรอบรูป ก็หาด้านเดียวก่อนโดยอาศัยอัตราส่วน sin (หรือเล่นท่ายาก กฎของ cos) เช่นเดิม เพียงแต่เปลี่ยนมุมตรงกลางจาก 360°/n มาเป็น 360°k/n ส่วนจำนวนด้านทั้งหมดที่จะต้องคูณ ก็มี n ด้านเหมือนเดิมครับ

หลายคนคงจะนึกออกแล้วล่ะครับ ว่าคำตอบก็ก๊อปจากเมื่อวานมาได้เลย นั่นคือ n d sin(180°k/n) ครับ ตรงนี้มองในใจได้อีกแล้ว จะเห็นว่าสูตรที่ได้นี้ก็ครอบคลุมกรณีรูปเหลี่ยมด้านเท่า (k=1) ด้วยเช่นกัน.. อ้าว งั้นคำตอบทั้งหมดที่อุตส่าห์นั่งคิดเมื่อวานก็ไม่ได้เอาไปใช้เลยอ่ะสิ เวรกรรม! :P
หลังจากได้คำตอบครบถ้วนแล้ว ทีนี้ถ้าใครให้เราหาเส้นรอบรูป n เหลี่ยม หรือดาว n แฉก (ที่แนบในวงกลมได้) เราก็แค่หยิบไม้บรรทัดมาวัดเส้นผ่านศูนย์กลางวงกลม แล้วแทนค่าลงในสูตรนี้ตอบได้เลยครับ เจ๋งมั้ยล่ะ!! (แต่ถ้าเรามีไม้บรรทัดจริงๆ เอามาวัดความยาว 1 ด้านแล้วคูณด้วย n ซะเลย จะไม่ดีกว่าเหรอเนี่ย อิๆๆ)
เพื่อไม่ให้บทความตอนนี้ยืดเกินไป ผมก็จะขอตัดจบดื้อๆ ห้วนๆ แต่เพียงเท่านี้เลยครับ พบกันใหม่ตอนต่อไปในวันพรุ่งนี้ ซึ่งก็จะยังคงแนะหลักการเรียนเลขโดยอาศัยโจทย์เพียงข้อเดียวเหมือนเดิมคร้าบ (คราวนี้จะเอาตัวอย่างที่ง่ายสุดๆ แล้วล่ะ) ^ ^
นวย 17/10/54 01:59
edit 31/3/2017 : เปลี่ยนคำตอบจากเดิมในรูป cos มาเป็น sin ตามบทความที่แล้วคร้าบ ^ ^
นวย 01/04/60 03:13 [ 1 ]