Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0440 จาก 0508
| กระทู้ที่ 0439 บทความ#3 : จะไปเป็นดาวโดดเด่น.. ได้ยังไง! | ตั้งกระทู้ใหม่ | กระทู้ที่ 0441 บทความ#5 : ใช้เวลาว่างให้เป็นจุดจุดจุด |
บทความ#4 : (แค่)คุณคุ้นคูณตอบ: 0, อ่าน: 2380
เมื่อวานเขียนถึงโจทย์แปลกๆ ไปแล้ว ได้เสียงตอบรับอย่างกริบทีเดียว วันนี้เราจึงมาดูโจทย์สั้นๆ ง่ายๆ กันบ้างดีกว่าครับ ผมขอเอาของเก่าที่เคยเขียนไว้มาหากินอีกรอบนึงก็แล้วกัน
นี่คือจุดเริ่มต้นของการ "สอนให้รู้หลักการเรียนเลข โดยอาศัยโจทย์เพียงข้อเดียว" ซึ่งผมทดลองเขียนลงในแฟนเพจตั้งแต่ 6 เดือนที่แล้ว และดูจะใช้การได้อยู่ครับ (หลายคนคงเคยอ่านแล้ว แต่อันนี้เป็นเวอร์ชั่นอัพเกรด โดยไปเอาเรื่องที่เคยเขียนไว้ที่อื่นมาเสริมให้มันยาวขึ้น) เอ้า เรามาเริ่มกันเลยดีกว่า!
==================================================
คนรอบข้างจะรู้ว่าผมชอบยกสถานการณ์ หรือขยันอุปมาอุปมัยเหลือเกิน เวลาจะสื่อสารถึงประเด็นใดๆ (เพราะกลัวพูดตรงไปตรงมาแล้วคนฟังจะไม่เห็นภาพ ไม่เข้าใจอารมณ์) วันนี้ผมอยากลองแนะนำการเรียนเลขโดยเล่าแบบใช้ตัวอย่างเปรียบเทียบดูบ้างครับ ซึ่งก็ไม่รู้จะทำให้งงยิ่งขึ้นหรือเปล่านะ ฮ่าๆๆ
พอดีผมไปเจอโจทย์ที่ต้อง "หาผลคูณ 7.5 x 48" เข้า ทำให้ความคิดไถลไปไกล
แต่ก่อนจะเล่าให้ฟัง อยากให้น้องๆ ที่อ่านอยู่ช่วยหาคำตอบเอาไว้ก่อนครับว่าได้เท่าไหร่ จะได้อ่านต่อรู้เรื่อง (ย้ำ! ต้องรู้คำตอบก่อนนะครับ สิ่งที่จะเขียนต่อไปถึงมีความหมาย) สมมติว่านี่เป็นเวลาสอบก็แล้วกัน เอ้าเริ่มเลยครับ..
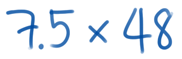
...
...
...
ได้คำตอบแล้วใช่ไหมครับ?
ผมว่าแต่ละคนคงมีวิธีคิดต่างกันไปตามถนัด ซึ่งโดยมากคงหยิบกระดาษปากกามาตั้งคูณ หรือบางคนสามารถคิดในใจได้โดยอาศัยเทคนิคบางอย่าง หรือพึ่งสูตรสำเร็จแบบเลขคณิตคิดไว แต่บางคนที่ขี้เกียจทดก็หยิบเครื่องคิดเลขขึ้นมากดซะเลย ซึ่งยุคนี้น่าจะเป็นอาการนี้กันเยอะอยู่นะครับ เห็นเวลาเรียนพยายามจะหยิบโทรศัพท์ขึ้นมาคิดเลขกันเหลือเกิน :P
สำหรับคนที่เมื่อกี๊ทดในกระดาษหรือแอบโกงกดเครื่องคิดเลข ผมจะให้ลองคิดในใจดูครับ ไม่ยากหรอก ขอใบ้แบบอ้อมๆ ก่อนว่า "ถ้าเปลี่ยนโจทย์เป็น 0.75 x 48 จะคิดในใจได้นะ" ถึงตรงนี้นึกออกหรือยังครับว่าทำยังไง (อ่ะให้เวลานึก 5 วินาที)
...
...
...
ถ้ายังนึกไม่ออก ขอบอกเพิ่มอีกนิดว่า ค่า 0.75 หรือว่า 75% เนี่ย เทียบได้กับเศษส่วนง่ายๆ จำนวนนึง (นึกออกหรือยังคร้าบ ใบ้สุดๆ ละนะ.. // ปรากฏว่าพี่ยิ่งใบ้ น้องก็ใบ้เหมือนกัน ฮ่าๆ)
...
...
...
เฉลยแล้วนะครับ!
เรารู้ว่าค่าของ 0.75 ก็คือ 3/4 นั่นเอง
ดังนั้น "0.75 x 48" ก็เลยคิดได้จาก 3/4 x 48 ซึ่งมันเป็นตัวเลขที่เราสามารถตัดในใจได้สบายๆ
แนะนำให้หารก่อนนะครับ ได้เป็น 12 แล้วค่อยมาคูณ 3 ..ได้คำตอบเท่ากับ 36
ฉะนั้นโจทย์ที่ว่า 7.5 x 48 ก็ต้องตอบว่า 360 ครับ
นี่คือเทคนิคที่ผมหาคำตอบของข้อนี้ได้ในใจ ซึ่งจะเห็นว่าทุกคนสามารถคิดแบบนี้ได้หมดเลย ไม่ต้องพึ่งกระดาษ ไม่ต้องพึ่งพวกสูตรคณิตคิดเร็ว และที่สำคัญ เร็วกว่าหันไปหยิบเครื่องคิดเลขอีกนะเนี่ย ^ ^
สำหรับประเด็นที่อยากจะเล่าวันนี้ก็คือ น้องๆ นักเรียนแต่ละคนมีระดับความเร็วไม่เท่ากันครับ ถ้ายกโจทย์การคูณข้อนี้เป็นตัวอย่าง ก็อาจจะแบ่งได้แบบนี้ (เรียงเป็นระดับคะแนนมากไปน้อยละกันนะครับ)
4 = คนที่คิดในใจโดยทำเป็นเศษส่วนได้เอง ไม่ต้องบอกใบ้เลย
3 = คนที่เมื่อฟังคำใบ้ว่า 0.75 ก็ปิ๊งไอเดียขึ้นมา คิดต่อเองได้จนจบ
2 = คนที่ต้องใบ้ไปอีก จนถึงคำว่า "ทำเป็นเศษส่วน" จึงจะคิดต่อได้
1 = คนที่ฟังไปเรื่อยๆ จนถึงคำตอบสุดท้ายแล้วทึ่ง พี่คิดวิธีนี้ได้ยังไงอ่ะ!
0 = คนที่อ่านมาจนถึงบรรทัดนี้ยังไม่รู้เรื่องอะไรกับเค้าเลย (ฮา)
อยากให้น้องๆ ที่อ่านอยู่ ลองย้อนนึกถึงเมื่อกี๊ดูว่าตัวเองอยู่ในระดับไหนนะครับ แล้วจากนี้ก็พยายามฝึกฝน โดยเฉพาะอย่างยิ่งเพิ่มการสังเกตเข้าไปในการเรียนเลขอีกนิด เพื่อทำให้ตัวเองขยับขึ้นไปอยู่ระดับบนขึ้นทีละขั้นๆ ให้ได้ เพราะการสังเกตควบคู่ไปกับการเรียนรู้สิ่งใหม่ จะทำให้เราคุ้นเคยกับวิชามากยิ่งขึ้น และงัดออกมาใช้ได้เมื่อถึงเวลาที่ต้องการ
พูดง่ายๆ ก็คือ "มีความรู้อย่างเดียวไม่ได้ ต้องคล่องด้วย" คงเหมือนที่ผู้ใหญ่เขาชอบพูดว่าอย่าฉลาดอย่างเดียว ต้องเฉลียวด้วย หรืออย่ารู้แต่สิ่งที่อยู่ในตำราอย่างเดียว ต้องประยุกต์เป็นด้วย นั่นแหละครับ
ตอนที่โพสเรื่องนี้ในแฟนเพจ มีผู้อ่านหลายคนบอกว่าคิดด้วยวิธีอื่น เช่น ทบค่าจาก 48 มาไว้ที่ 7.5 กลายเป็น 15 x 24 หรือถ้าทบอีกทีก็เป็น 30 x 12 = 360 ..วิธีนี้ก็แจ่มครับ ยกให้เป็นระดับ 3.5 ถึง 4 ได้เหมือนกัน อิๆๆ
อ้าวแล้วถ้าคิดในใจด้วยเทคนิคพวกเลขคณิตคิดไวล่ะ (เช่น ลงท้ายด้วย 5 จะหาผลคูณได้โดยเอาตัวนี้ไปบวกตัวโน้น แล้วต่อท้ายด้วยตัวนั้น ฯลฯ) ..โอเคในที่นี้ต้องยอมรับว่าเจ๋งมาก และขอยกให้เป็นระดับ 5 เลยละกันครับ (เอ๊ะเกิน max หรือเปล่า) แต่ขอเตือนว่าในการทำข้อสอบจริงๆ ที่ไม่ใช่การคูณเลขแบบนี้ การพึ่งสูตรสำเร็จไม่ใช่วิธีที่ดีกับชีวิตเลยล่ะครับ โดยเฉพาะคนที่ไม่มีความรู้มาก่อนเลย แล้วสักแต่ว่าท่องจำ อันนี้เดี๋ยวได้ตกไปอยู่ระดับ 0 แน่นอน :P
ปัญหาของการยกตัวอย่างเปรียบเปรยที่ผมชอบทำนั้น คือผู้อ่านอาจคิดว่าผมตั้งใจจะบอกเรื่องนั้นเรื่องเดียว ไม่ได้คิดว่ามีแกนเรื่องที่อยากสื่ออยู่เบื้องหลัง (เช่นในบทความตอนแรก อาจจะมีใครคิดว่าผมเขียนเพื่อต่อต้านการใช้ Math E-Book ในการสอนเท่านั้น ซึ่งมันไม่ใช่ครับ ประเด็นที่จะบอกคือไม่ว่างานอะไรขอให้ตั้งใจทำให้สุดต่างหาก เพียงแต่หยิบยกตัวอย่างด้วยเรื่องการสอนเลข) ฉะนั้นบทความตอนนี้จึงต้องขอเน้นซะหน่อยว่า ผมไม่ได้เขียนเพื่อให้ทุกคนไปหัดคูณเลขเร็วนะครับ ^ ^
เพราะแม้ที่ยกตัวอย่างมานี้จะเป็นเพียงโจทย์คูณเลขแบบประถม แต่รู้ไหมครับว่าข้อสอบ ม.ปลาย จำนวนมากก็มีลักษณะคล้ายแบบนี้ คือมีวิธีไปถึงคำตอบได้หลายทาง ใครที่เข้าใจลึกซึ้งก็จะคิดได้แบบสั้นๆ ง่ายๆ ส่วนใครที่พอรู้บ้างก็ยังสามารถคิดแบบลุยไปทื่อๆ แล้วได้คำตอบเหมือนกัน แต่จะเสียเวลากว่า และอาจทำข้อสอบทั้งฉบับไม่ทันเวลา
ซึ่งส่วนตัวผมชอบข้อสอบลักษณะนี้นะครับ เพราะจะให้คะแนนมากหน่อยสำหรับผู้ที่ทำได้ไว ทันเวลา ในขณะเดียวกันก็ไม่ได้ตัดโอกาสที่จะได้คะแนนของผู้ที่คิดวิธีทื่อๆ หรือคิดอ้อมโลกไปบ้าง
จากบทความนี้ สิ่งที่น้องๆ น่าเก็บไปคิดคือ "ทำไมเพื่อนบางคนถึงรู้ว่าข้อนั้นๆ ต้องคิดแบบนั้น แต่เรากลับนึกไม่ออก ทั้งที่ก็เรียนมาเท่ากัน.." ไม่ได้เจาะจงว่าต้องเป็นเรื่องการคูณเลขแล้วนะครับ จะเป็นโจทย์เรื่องอะไรก็ได้ จะเห็นความแตกต่างของแต่ละคนเป็นระดับๆ อย่างที่เล่ามา
ถ้าใครเข้าใจแก่นที่ผมอยากสื่อสารแล้ว สามารถเอาสิ่งนี้เป็นจุดมุ่งหมายของการเรียนที่ ร.ร. ได้เลยล่ะครับ ผมเพียงต้องการชี้ให้เห็นว่า เราทำความเข้าใจในวิชาอย่างเดียวไม่พอครับ การฝึกฝน สังเกต และงัดวิธีดีๆ ออกมาใช้ได้ทันเวลาก็สำคัญไม่แพ้กันครับ ^ ^
==================================================
..มาถึงตอนนี้ผมก็นึกขึ้นได้ว่าเคยเขียนบทความในประเด็นคล้ายๆ กัน เมื่อ 8 ปีก่อน ในชื่อเรื่อง "แค่เข้าใจไม่พอใช้สอบ!" เพื่อจะตอบปัญหาของน้องๆ ที่ว่า "ก็เรียนเข้าใจนะ แต่ทำไมไม่เห็นจะสอบได้ดีซะที"
นั่นก็เพราะน้องๆ ยังขาดสิ่งหนึ่งที่เรียกว่า "ความคุ้นเคย" ไงครับ
ความคุ้นเคยคือสิ่งจำเป็นสำหรับการสอบทุกวิชา ไม่อย่างงั้นทำเสร็จไม่ทันเวลาแน่นอน การที่เราจะตอบปัญหาในข้อสอบได้ดี นอกจากเราจะเข้าใจเนื้อหาทั้งหมด เรายังต้อง "คุ้นเคย" กับมัน ชนิดที่ว่าปิ๊งขึ้นมาได้ในทันทีด้วย ไม่ใช่ออกจากห้องสอบแล้วเพิ่งมานึกได้ เอ๊ะทำไมเมื่อกี๊ไม่ตอบไปว่าอย่างงี้ฟระ! ..แถมความคุ้นเคยยังช่วยให้เราอ่านหนังสือได้เร็วขึ้นด้วยนะครับ เพราะมันเป็นการทบทวนสิ่งที่เราคุ้นอยู่แล้ว
ผมเพิ่งจะเห็นว่า การฝึกฝน สังเกต เพื่องัดวิธีดีๆ ออกมาใช้ หรือที่เรียกว่าต้อง "คล่อง" ดังที่เล่ามาข้างบนทั้งหมด ก็ถือเป็นความ "คุ้นเคย" ในแบบฉบับของวิชาคณิตศาสตร์นั่นเองครับ
แต่ที่จริงแล้วไม่ว่าวิชาไหน เราก็มีวิธีสร้างความคุ้นเคยได้ด้วยวิธีคล้ายๆ กัน จึงขอพูดเผื่อวิชาอื่นไปเลยนะครับ เช่น ตอนเรียนก็เอาใจเข้าไปใส่ซะหน่อย รู้จักคิดตาม และเก็บไปคิดต่อ รู้จักเสาะหาที่มา (เป็นมายังไง หลักการอย่างไร) แล้วก็ที่ไป (เอาไปใช้ยังไง มีประโยชน์ตรงไหน) และที่สำคัญ การฝึกฝนจริง ทดลองจริง จะทำให้ได้ประสบการณ์ซึ่งช่วยเพิ่มความคุ้นเคยได้อย่างดีครับ
ในบทความดังกล่าวผมได้ยกตัวอย่างจริงๆ มาเปรียบเทียบ เป็นนาย A กับนาย B ไว้อีกแล้ว สงสัยจะมีอยู่มุขเดียวแฮะ 555
นาย A ตั้งใจอ่านหนังสือมาก ฟังอาจารย์และจดตามยิกๆ ไม่เคยพลาดสักประโยค เขาขยันอ่านหนังสือจนจำทุกคำพูดได้ขึ้นใจ แต่พอเข้าห้องสอบ ถ้าเจอโจทย์ที่ไม่ใช่การถามตรงไปตรงมาว่าอะไรคืออะไร แต่มีปัญหามาให้คิดวิธีแก้ นาย A อาจจะอึ้ง ไม่รู้จะหยิบความรู้ส่วนไหนมาใช้ดี ทั้งที่อัดมาอย่างแน่นสมองเลย
เพราะเขาแค่ "รู้" แต่ยังไม่ "คุ้นเคย" ครับ
เหมือนแบกอุปกรณ์มาสอบ 20 ชิ้น แต่ไม่รู้อันไหนใช้ยังไง หรือรู้แล้วแต่ยังไม่เคยลองใช้ มันก็ช้าสิครับ!
ขณะที่นาย B ตอนเรียนอาจจะไม่ตั้งใจฟังไปบ้าง แต่เขารู้จักใช้จินตนาการ ปะติดปะต่อ เรื่องราวเป็นมายังไง แล้วเอาไปใช้อะไรยังไง หรือถ้าปรับเปลี่ยนไปนิดแล้วจะเกิดอะไรขึ้น เรียกว่าคิดเอาสนุกไปเรื่อยเปื่อย ถ้ามีใครพูดถึงเรื่องไหนขึ้นมา ความรู้ที่เขามีก็จะพรั่งพรูออกมาได้เป็นฉากๆ
งานนี้นาย B อาจจะทำคะแนนสอบได้ดีกว่านาย A ก็ได้ครับ เพราะแม้เขาจะรู้ไม่มากเท่า แต่ทุกอย่างที่เขารู้ล้วนส่งผลได้แต้มหมดเลย
ขอออกตัวว่านี่ผมไม่ได้เชียร์น้องๆ ว่าไม่จำเป็นต้องฟังครูนะครับ ในตัวอย่างนี้มีทั้งข้อดีและข้อเสียทั้งคู่ และได้ผลไม่เท่ากัน ซึ่งอย่างน้อยนาย A ก็คงได้คะแนนไปประมาณหนึ่ง แถมยังเก็บจิตพิสัยเต็มอีกด้วย ไม่อยากได้เหรอครับ อิๆๆ ส่วนนาย B ที่ไม่ค่อยตั้งใจฟังแล้วดันได้คะแนนดี ก็เพราะการสอบคือการวัดผลความรู้ความเข้าใจในวิชา และนาย B ก็แอบไปทำความเข้าใจมาจริงๆ อย่าไปโกรธเขานะครับ (ฮา)
ส่วนใครที่ทั้งไม่ตั้งใจฟังครูสอนด้วยและไม่เอาใจเข้าไปใส่ในวิชาด้วย อันนี้ก็ตัวใครตัวมันล่ะคร้าบ แฮ่!
ตอนต่อไปในวันพรุ่งนี้ ผมจะมาตอบคำถามอีกข้อที่ว่า "อะไรที่เรียกว่าใช้เวลาว่างช่วงปิดเทอมให้เป็นประโยชน์?" ซึ่งคงไม่ใช่การนั่งอ่านหนังสือเรียน หรือไปสมัครเป็นพนักงานร้านแมคฯ แน่นอน มันจะระเบียบรัดเกิ๊น! ..แล้วอย่าลืมติดตามกันต่อนะคร้าบ ^ ^
นี่คือจุดเริ่มต้นของการ "สอนให้รู้หลักการเรียนเลข โดยอาศัยโจทย์เพียงข้อเดียว" ซึ่งผมทดลองเขียนลงในแฟนเพจตั้งแต่ 6 เดือนที่แล้ว และดูจะใช้การได้อยู่ครับ (หลายคนคงเคยอ่านแล้ว แต่อันนี้เป็นเวอร์ชั่นอัพเกรด โดยไปเอาเรื่องที่เคยเขียนไว้ที่อื่นมาเสริมให้มันยาวขึ้น) เอ้า เรามาเริ่มกันเลยดีกว่า!
==================================================
คนรอบข้างจะรู้ว่าผมชอบยกสถานการณ์ หรือขยันอุปมาอุปมัยเหลือเกิน เวลาจะสื่อสารถึงประเด็นใดๆ (เพราะกลัวพูดตรงไปตรงมาแล้วคนฟังจะไม่เห็นภาพ ไม่เข้าใจอารมณ์) วันนี้ผมอยากลองแนะนำการเรียนเลขโดยเล่าแบบใช้ตัวอย่างเปรียบเทียบดูบ้างครับ ซึ่งก็ไม่รู้จะทำให้งงยิ่งขึ้นหรือเปล่านะ ฮ่าๆๆ
พอดีผมไปเจอโจทย์ที่ต้อง "หาผลคูณ 7.5 x 48" เข้า ทำให้ความคิดไถลไปไกล
แต่ก่อนจะเล่าให้ฟัง อยากให้น้องๆ ที่อ่านอยู่ช่วยหาคำตอบเอาไว้ก่อนครับว่าได้เท่าไหร่ จะได้อ่านต่อรู้เรื่อง (ย้ำ! ต้องรู้คำตอบก่อนนะครับ สิ่งที่จะเขียนต่อไปถึงมีความหมาย) สมมติว่านี่เป็นเวลาสอบก็แล้วกัน เอ้าเริ่มเลยครับ..
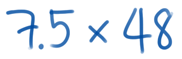
...
...
...
ได้คำตอบแล้วใช่ไหมครับ?
ผมว่าแต่ละคนคงมีวิธีคิดต่างกันไปตามถนัด ซึ่งโดยมากคงหยิบกระดาษปากกามาตั้งคูณ หรือบางคนสามารถคิดในใจได้โดยอาศัยเทคนิคบางอย่าง หรือพึ่งสูตรสำเร็จแบบเลขคณิตคิดไว แต่บางคนที่ขี้เกียจทดก็หยิบเครื่องคิดเลขขึ้นมากดซะเลย ซึ่งยุคนี้น่าจะเป็นอาการนี้กันเยอะอยู่นะครับ เห็นเวลาเรียนพยายามจะหยิบโทรศัพท์ขึ้นมาคิดเลขกันเหลือเกิน :P
สำหรับคนที่เมื่อกี๊ทดในกระดาษหรือแอบโกงกดเครื่องคิดเลข ผมจะให้ลองคิดในใจดูครับ ไม่ยากหรอก ขอใบ้แบบอ้อมๆ ก่อนว่า "ถ้าเปลี่ยนโจทย์เป็น 0.75 x 48 จะคิดในใจได้นะ" ถึงตรงนี้นึกออกหรือยังครับว่าทำยังไง (อ่ะให้เวลานึก 5 วินาที)
...
...
...
ถ้ายังนึกไม่ออก ขอบอกเพิ่มอีกนิดว่า ค่า 0.75 หรือว่า 75% เนี่ย เทียบได้กับเศษส่วนง่ายๆ จำนวนนึง (นึกออกหรือยังคร้าบ ใบ้สุดๆ ละนะ.. // ปรากฏว่าพี่ยิ่งใบ้ น้องก็ใบ้เหมือนกัน ฮ่าๆ)
...
...
...
เฉลยแล้วนะครับ!
เรารู้ว่าค่าของ 0.75 ก็คือ 3/4 นั่นเอง
ดังนั้น "0.75 x 48" ก็เลยคิดได้จาก 3/4 x 48 ซึ่งมันเป็นตัวเลขที่เราสามารถตัดในใจได้สบายๆ
แนะนำให้หารก่อนนะครับ ได้เป็น 12 แล้วค่อยมาคูณ 3 ..ได้คำตอบเท่ากับ 36
ฉะนั้นโจทย์ที่ว่า 7.5 x 48 ก็ต้องตอบว่า 360 ครับ
นี่คือเทคนิคที่ผมหาคำตอบของข้อนี้ได้ในใจ ซึ่งจะเห็นว่าทุกคนสามารถคิดแบบนี้ได้หมดเลย ไม่ต้องพึ่งกระดาษ ไม่ต้องพึ่งพวกสูตรคณิตคิดเร็ว และที่สำคัญ เร็วกว่าหันไปหยิบเครื่องคิดเลขอีกนะเนี่ย ^ ^
สำหรับประเด็นที่อยากจะเล่าวันนี้ก็คือ น้องๆ นักเรียนแต่ละคนมีระดับความเร็วไม่เท่ากันครับ ถ้ายกโจทย์การคูณข้อนี้เป็นตัวอย่าง ก็อาจจะแบ่งได้แบบนี้ (เรียงเป็นระดับคะแนนมากไปน้อยละกันนะครับ)
4 = คนที่คิดในใจโดยทำเป็นเศษส่วนได้เอง ไม่ต้องบอกใบ้เลย
3 = คนที่เมื่อฟังคำใบ้ว่า 0.75 ก็ปิ๊งไอเดียขึ้นมา คิดต่อเองได้จนจบ
2 = คนที่ต้องใบ้ไปอีก จนถึงคำว่า "ทำเป็นเศษส่วน" จึงจะคิดต่อได้
1 = คนที่ฟังไปเรื่อยๆ จนถึงคำตอบสุดท้ายแล้วทึ่ง พี่คิดวิธีนี้ได้ยังไงอ่ะ!
0 = คนที่อ่านมาจนถึงบรรทัดนี้ยังไม่รู้เรื่องอะไรกับเค้าเลย (ฮา)
อยากให้น้องๆ ที่อ่านอยู่ ลองย้อนนึกถึงเมื่อกี๊ดูว่าตัวเองอยู่ในระดับไหนนะครับ แล้วจากนี้ก็พยายามฝึกฝน โดยเฉพาะอย่างยิ่งเพิ่มการสังเกตเข้าไปในการเรียนเลขอีกนิด เพื่อทำให้ตัวเองขยับขึ้นไปอยู่ระดับบนขึ้นทีละขั้นๆ ให้ได้ เพราะการสังเกตควบคู่ไปกับการเรียนรู้สิ่งใหม่ จะทำให้เราคุ้นเคยกับวิชามากยิ่งขึ้น และงัดออกมาใช้ได้เมื่อถึงเวลาที่ต้องการ
พูดง่ายๆ ก็คือ "มีความรู้อย่างเดียวไม่ได้ ต้องคล่องด้วย" คงเหมือนที่ผู้ใหญ่เขาชอบพูดว่าอย่าฉลาดอย่างเดียว ต้องเฉลียวด้วย หรืออย่ารู้แต่สิ่งที่อยู่ในตำราอย่างเดียว ต้องประยุกต์เป็นด้วย นั่นแหละครับ
ตอนที่โพสเรื่องนี้ในแฟนเพจ มีผู้อ่านหลายคนบอกว่าคิดด้วยวิธีอื่น เช่น ทบค่าจาก 48 มาไว้ที่ 7.5 กลายเป็น 15 x 24 หรือถ้าทบอีกทีก็เป็น 30 x 12 = 360 ..วิธีนี้ก็แจ่มครับ ยกให้เป็นระดับ 3.5 ถึง 4 ได้เหมือนกัน อิๆๆ
อ้าวแล้วถ้าคิดในใจด้วยเทคนิคพวกเลขคณิตคิดไวล่ะ (เช่น ลงท้ายด้วย 5 จะหาผลคูณได้โดยเอาตัวนี้ไปบวกตัวโน้น แล้วต่อท้ายด้วยตัวนั้น ฯลฯ) ..โอเคในที่นี้ต้องยอมรับว่าเจ๋งมาก และขอยกให้เป็นระดับ 5 เลยละกันครับ (เอ๊ะเกิน max หรือเปล่า) แต่ขอเตือนว่าในการทำข้อสอบจริงๆ ที่ไม่ใช่การคูณเลขแบบนี้ การพึ่งสูตรสำเร็จไม่ใช่วิธีที่ดีกับชีวิตเลยล่ะครับ โดยเฉพาะคนที่ไม่มีความรู้มาก่อนเลย แล้วสักแต่ว่าท่องจำ อันนี้เดี๋ยวได้ตกไปอยู่ระดับ 0 แน่นอน :P
ปัญหาของการยกตัวอย่างเปรียบเปรยที่ผมชอบทำนั้น คือผู้อ่านอาจคิดว่าผมตั้งใจจะบอกเรื่องนั้นเรื่องเดียว ไม่ได้คิดว่ามีแกนเรื่องที่อยากสื่ออยู่เบื้องหลัง (เช่นในบทความตอนแรก อาจจะมีใครคิดว่าผมเขียนเพื่อต่อต้านการใช้ Math E-Book ในการสอนเท่านั้น ซึ่งมันไม่ใช่ครับ ประเด็นที่จะบอกคือไม่ว่างานอะไรขอให้ตั้งใจทำให้สุดต่างหาก เพียงแต่หยิบยกตัวอย่างด้วยเรื่องการสอนเลข) ฉะนั้นบทความตอนนี้จึงต้องขอเน้นซะหน่อยว่า ผมไม่ได้เขียนเพื่อให้ทุกคนไปหัดคูณเลขเร็วนะครับ ^ ^
เพราะแม้ที่ยกตัวอย่างมานี้จะเป็นเพียงโจทย์คูณเลขแบบประถม แต่รู้ไหมครับว่าข้อสอบ ม.ปลาย จำนวนมากก็มีลักษณะคล้ายแบบนี้ คือมีวิธีไปถึงคำตอบได้หลายทาง ใครที่เข้าใจลึกซึ้งก็จะคิดได้แบบสั้นๆ ง่ายๆ ส่วนใครที่พอรู้บ้างก็ยังสามารถคิดแบบลุยไปทื่อๆ แล้วได้คำตอบเหมือนกัน แต่จะเสียเวลากว่า และอาจทำข้อสอบทั้งฉบับไม่ทันเวลา
ซึ่งส่วนตัวผมชอบข้อสอบลักษณะนี้นะครับ เพราะจะให้คะแนนมากหน่อยสำหรับผู้ที่ทำได้ไว ทันเวลา ในขณะเดียวกันก็ไม่ได้ตัดโอกาสที่จะได้คะแนนของผู้ที่คิดวิธีทื่อๆ หรือคิดอ้อมโลกไปบ้าง
จากบทความนี้ สิ่งที่น้องๆ น่าเก็บไปคิดคือ "ทำไมเพื่อนบางคนถึงรู้ว่าข้อนั้นๆ ต้องคิดแบบนั้น แต่เรากลับนึกไม่ออก ทั้งที่ก็เรียนมาเท่ากัน.." ไม่ได้เจาะจงว่าต้องเป็นเรื่องการคูณเลขแล้วนะครับ จะเป็นโจทย์เรื่องอะไรก็ได้ จะเห็นความแตกต่างของแต่ละคนเป็นระดับๆ อย่างที่เล่ามา
ถ้าใครเข้าใจแก่นที่ผมอยากสื่อสารแล้ว สามารถเอาสิ่งนี้เป็นจุดมุ่งหมายของการเรียนที่ ร.ร. ได้เลยล่ะครับ ผมเพียงต้องการชี้ให้เห็นว่า เราทำความเข้าใจในวิชาอย่างเดียวไม่พอครับ การฝึกฝน สังเกต และงัดวิธีดีๆ ออกมาใช้ได้ทันเวลาก็สำคัญไม่แพ้กันครับ ^ ^
==================================================
..มาถึงตอนนี้ผมก็นึกขึ้นได้ว่าเคยเขียนบทความในประเด็นคล้ายๆ กัน เมื่อ 8 ปีก่อน ในชื่อเรื่อง "แค่เข้าใจไม่พอใช้สอบ!" เพื่อจะตอบปัญหาของน้องๆ ที่ว่า "ก็เรียนเข้าใจนะ แต่ทำไมไม่เห็นจะสอบได้ดีซะที"
นั่นก็เพราะน้องๆ ยังขาดสิ่งหนึ่งที่เรียกว่า "ความคุ้นเคย" ไงครับ
ความคุ้นเคยคือสิ่งจำเป็นสำหรับการสอบทุกวิชา ไม่อย่างงั้นทำเสร็จไม่ทันเวลาแน่นอน การที่เราจะตอบปัญหาในข้อสอบได้ดี นอกจากเราจะเข้าใจเนื้อหาทั้งหมด เรายังต้อง "คุ้นเคย" กับมัน ชนิดที่ว่าปิ๊งขึ้นมาได้ในทันทีด้วย ไม่ใช่ออกจากห้องสอบแล้วเพิ่งมานึกได้ เอ๊ะทำไมเมื่อกี๊ไม่ตอบไปว่าอย่างงี้ฟระ! ..แถมความคุ้นเคยยังช่วยให้เราอ่านหนังสือได้เร็วขึ้นด้วยนะครับ เพราะมันเป็นการทบทวนสิ่งที่เราคุ้นอยู่แล้ว
ผมเพิ่งจะเห็นว่า การฝึกฝน สังเกต เพื่องัดวิธีดีๆ ออกมาใช้ หรือที่เรียกว่าต้อง "คล่อง" ดังที่เล่ามาข้างบนทั้งหมด ก็ถือเป็นความ "คุ้นเคย" ในแบบฉบับของวิชาคณิตศาสตร์นั่นเองครับ
แต่ที่จริงแล้วไม่ว่าวิชาไหน เราก็มีวิธีสร้างความคุ้นเคยได้ด้วยวิธีคล้ายๆ กัน จึงขอพูดเผื่อวิชาอื่นไปเลยนะครับ เช่น ตอนเรียนก็เอาใจเข้าไปใส่ซะหน่อย รู้จักคิดตาม และเก็บไปคิดต่อ รู้จักเสาะหาที่มา (เป็นมายังไง หลักการอย่างไร) แล้วก็ที่ไป (เอาไปใช้ยังไง มีประโยชน์ตรงไหน) และที่สำคัญ การฝึกฝนจริง ทดลองจริง จะทำให้ได้ประสบการณ์ซึ่งช่วยเพิ่มความคุ้นเคยได้อย่างดีครับ
ในบทความดังกล่าวผมได้ยกตัวอย่างจริงๆ มาเปรียบเทียบ เป็นนาย A กับนาย B ไว้อีกแล้ว สงสัยจะมีอยู่มุขเดียวแฮะ 555
นาย A ตั้งใจอ่านหนังสือมาก ฟังอาจารย์และจดตามยิกๆ ไม่เคยพลาดสักประโยค เขาขยันอ่านหนังสือจนจำทุกคำพูดได้ขึ้นใจ แต่พอเข้าห้องสอบ ถ้าเจอโจทย์ที่ไม่ใช่การถามตรงไปตรงมาว่าอะไรคืออะไร แต่มีปัญหามาให้คิดวิธีแก้ นาย A อาจจะอึ้ง ไม่รู้จะหยิบความรู้ส่วนไหนมาใช้ดี ทั้งที่อัดมาอย่างแน่นสมองเลย
เพราะเขาแค่ "รู้" แต่ยังไม่ "คุ้นเคย" ครับ
เหมือนแบกอุปกรณ์มาสอบ 20 ชิ้น แต่ไม่รู้อันไหนใช้ยังไง หรือรู้แล้วแต่ยังไม่เคยลองใช้ มันก็ช้าสิครับ!
ขณะที่นาย B ตอนเรียนอาจจะไม่ตั้งใจฟังไปบ้าง แต่เขารู้จักใช้จินตนาการ ปะติดปะต่อ เรื่องราวเป็นมายังไง แล้วเอาไปใช้อะไรยังไง หรือถ้าปรับเปลี่ยนไปนิดแล้วจะเกิดอะไรขึ้น เรียกว่าคิดเอาสนุกไปเรื่อยเปื่อย ถ้ามีใครพูดถึงเรื่องไหนขึ้นมา ความรู้ที่เขามีก็จะพรั่งพรูออกมาได้เป็นฉากๆ
งานนี้นาย B อาจจะทำคะแนนสอบได้ดีกว่านาย A ก็ได้ครับ เพราะแม้เขาจะรู้ไม่มากเท่า แต่ทุกอย่างที่เขารู้ล้วนส่งผลได้แต้มหมดเลย
ขอออกตัวว่านี่ผมไม่ได้เชียร์น้องๆ ว่าไม่จำเป็นต้องฟังครูนะครับ ในตัวอย่างนี้มีทั้งข้อดีและข้อเสียทั้งคู่ และได้ผลไม่เท่ากัน ซึ่งอย่างน้อยนาย A ก็คงได้คะแนนไปประมาณหนึ่ง แถมยังเก็บจิตพิสัยเต็มอีกด้วย ไม่อยากได้เหรอครับ อิๆๆ ส่วนนาย B ที่ไม่ค่อยตั้งใจฟังแล้วดันได้คะแนนดี ก็เพราะการสอบคือการวัดผลความรู้ความเข้าใจในวิชา และนาย B ก็แอบไปทำความเข้าใจมาจริงๆ อย่าไปโกรธเขานะครับ (ฮา)
ส่วนใครที่ทั้งไม่ตั้งใจฟังครูสอนด้วยและไม่เอาใจเข้าไปใส่ในวิชาด้วย อันนี้ก็ตัวใครตัวมันล่ะคร้าบ แฮ่!
ตอนต่อไปในวันพรุ่งนี้ ผมจะมาตอบคำถามอีกข้อที่ว่า "อะไรที่เรียกว่าใช้เวลาว่างช่วงปิดเทอมให้เป็นประโยชน์?" ซึ่งคงไม่ใช่การนั่งอ่านหนังสือเรียน หรือไปสมัครเป็นพนักงานร้านแมคฯ แน่นอน มันจะระเบียบรัดเกิ๊น! ..แล้วอย่าลืมติดตามกันต่อนะคร้าบ ^ ^
นวย 18/10/54 20:28