Math E-Book
Release 2.7pre2 + Conc!
Release 2.7pre2 + Conc!
กระทู้ที่ 0473 จาก 0508
| กระทู้ที่ 0472 ถามโจทย์หน่อยครับ | ตั้งกระทู้ใหม่ | กระทู้ที่ 0474 รบกวนด้วยครับ |
ขอถามโจทย์เรื่องเซตครับตอบ: 1, อ่าน: 4370
สำหรับเซต S ใดๆ ให้ S' แทนคอมพลีเมนต์ของเซต S
กำหนดให้ A, B และ C เป็นเซตในเอกภพสัมพัทธ์ U โดยที่ A intersect B = B
C เป็นซับเซตของ A และ B intersect C ไม่เท่ากับ เซตว่าง
ถ้าเซต U มีสมาชิก 12 ตัว เซต A' union B' มีสมาชิก 10 ตัว และเซต A intersect B'
มีสมาชิก 4 ตัว แล้วจะมีเซต C ทั้งหมดกี่เซต
1. 60 เซต
2. 48 เซต
3. 16 เซต
4. 8 เซต
เป็นกำลังใจให้พี่เสมอครับ ขอบคุณครับ
กำหนดให้ A, B และ C เป็นเซตในเอกภพสัมพัทธ์ U โดยที่ A intersect B = B
C เป็นซับเซตของ A และ B intersect C ไม่เท่ากับ เซตว่าง
ถ้าเซต U มีสมาชิก 12 ตัว เซต A' union B' มีสมาชิก 10 ตัว และเซต A intersect B'
มีสมาชิก 4 ตัว แล้วจะมีเซต C ทั้งหมดกี่เซต
1. 60 เซต
2. 48 เซต
3. 16 เซต
4. 8 เซต
เป็นกำลังใจให้พี่เสมอครับ ขอบคุณครับ
BooM 29/07/55 09:23
ข้อนี้ถ้าคิดเผินๆ น่าจะตอบ 48 เซต แต่พี่นวยมองว่าโจทย์ให้ข้อมูลไม่ชัดเจนนะครับ
โดยขั้นตอนการคิดเป็นแบบนี้ครับ
(๑) จาก A intersect B = B จะได้ว่า B เป็นสับเซตของ A
(๒) จาก C เป็นสับเซตของ A โดยที่ B intersect C ไม่เป็นเซตว่าง
นำไปเขียนแผนภาพไว้ก่อนเลยครับ สมมติว่า ก, ข, ค, ง, จ เป็นจำนวนสมาชิกแต่ละชิ้นส่วนละกัน
ในแผนภาพนี้ก็จะได้ข้อบังคับว่า ข ห้ามเป็น 0 ครับ
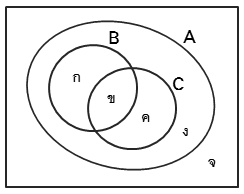
(๓) จาก n(A' u B') = 10 แต่เรารู้ว่าในที่นี้ A' u B' = B'
จึงกลายเป็น n(B') = 10 ..นั่นคือ n(B) = 12-10 = 2 ครับ >> (ก+ข = 2)
ถ้าสมมติว่ารู้หน้าตาของสมาชิก 12 ตัวและ 10 ตัวดังกล่าว* ก็จะรู้หน้าตาสมาชิก 2 ตัวที่จะอยู่ใน ก+ข
และจะสลับสมาชิกได้ 2 กรณี คือ ก=1,ข=1 (มีได้ 2 แบบ) และ ก=0,ข=2 (มีได้ 1 แบบ)
(๔) จาก n(A int B') = 4 >> (ค+ง = 4)
ถ้าสมมติว่ารู้หน้าตาของสมาชิก 4 ตัวที่จะอยู่ใน ค+ง ดังกล่าว* ก็จะเลือกสมาชิกได้ 2^4 แบบ
สรุป.. เซต C นั้นเกิดจากสมาชิกตรง ข กับ ค มารวมกัน
โดย ข มีหน้าตาต่างๆ ได้ 3 แบบ (จากข้อ ๓) และ ค มีหน้าตาต่างๆ ได้ 16 แบบ (จากข้อ ๔)
จึงนำมาประกอบกันเป็น C ได้ทั้งหมด 3 x 16 = 48 แบบครับ
* ข้อนี้ถือว่าเป็นโจทย์ที่ไอเดียดีเลยนะครับ แต่ติดที่ว่าให้ข้อมูลไม่ชัดเจน
ก็คือโจทย์ไม่ได้ระบุว่า "เรารู้หน้าตาสมาชิก" ตามที่พี่นวยได้สมมติไว้ครับ
แต่ถ้าไม่ทึกทักเองไปแบบนี้ก็คงจะไม่ได้คำตอบ เพราะจะเกิดเซต C ได้ไม่รู้จบคร้าบ :]
โดยขั้นตอนการคิดเป็นแบบนี้ครับ
(๑) จาก A intersect B = B จะได้ว่า B เป็นสับเซตของ A
(๒) จาก C เป็นสับเซตของ A โดยที่ B intersect C ไม่เป็นเซตว่าง
นำไปเขียนแผนภาพไว้ก่อนเลยครับ สมมติว่า ก, ข, ค, ง, จ เป็นจำนวนสมาชิกแต่ละชิ้นส่วนละกัน
ในแผนภาพนี้ก็จะได้ข้อบังคับว่า ข ห้ามเป็น 0 ครับ

(๓) จาก n(A' u B') = 10 แต่เรารู้ว่าในที่นี้ A' u B' = B'
จึงกลายเป็น n(B') = 10 ..นั่นคือ n(B) = 12-10 = 2 ครับ >> (ก+ข = 2)
ถ้าสมมติว่ารู้หน้าตาของสมาชิก 12 ตัวและ 10 ตัวดังกล่าว* ก็จะรู้หน้าตาสมาชิก 2 ตัวที่จะอยู่ใน ก+ข
และจะสลับสมาชิกได้ 2 กรณี คือ ก=1,ข=1 (มีได้ 2 แบบ) และ ก=0,ข=2 (มีได้ 1 แบบ)
(๔) จาก n(A int B') = 4 >> (ค+ง = 4)
ถ้าสมมติว่ารู้หน้าตาของสมาชิก 4 ตัวที่จะอยู่ใน ค+ง ดังกล่าว* ก็จะเลือกสมาชิกได้ 2^4 แบบ
สรุป.. เซต C นั้นเกิดจากสมาชิกตรง ข กับ ค มารวมกัน
โดย ข มีหน้าตาต่างๆ ได้ 3 แบบ (จากข้อ ๓) และ ค มีหน้าตาต่างๆ ได้ 16 แบบ (จากข้อ ๔)
จึงนำมาประกอบกันเป็น C ได้ทั้งหมด 3 x 16 = 48 แบบครับ
* ข้อนี้ถือว่าเป็นโจทย์ที่ไอเดียดีเลยนะครับ แต่ติดที่ว่าให้ข้อมูลไม่ชัดเจน
ก็คือโจทย์ไม่ได้ระบุว่า "เรารู้หน้าตาสมาชิก" ตามที่พี่นวยได้สมมติไว้ครับ
แต่ถ้าไม่ทึกทักเองไปแบบนี้ก็คงจะไม่ได้คำตอบ เพราะจะเกิดเซต C ได้ไม่รู้จบคร้าบ :]
นวย 17/08/55 19:59 [ 1 ]